A recent CodeGolf question defines "reverse addition" for two integers $a, b$ as follows: do normal "grade-school" addition, but from left-to-right (with leading zeroes as necessary) instead of right-to-left. As an example, consider 145 and 98, which has a summation setup as follows:
145
+ 98
-----
243
This is usual addition - now we do reverse addition:
145
+ 98
-----
1341
Since 1+0 = 1, we have the first entry is 1. Then we add 4+9 = 13, which has a carry of 1, and so the second entry is 3, the third is 4, and the last is 1 from the previous carry.
I will define the result of reverse addition for $a, b$ is $reverseadd(a, b)$.
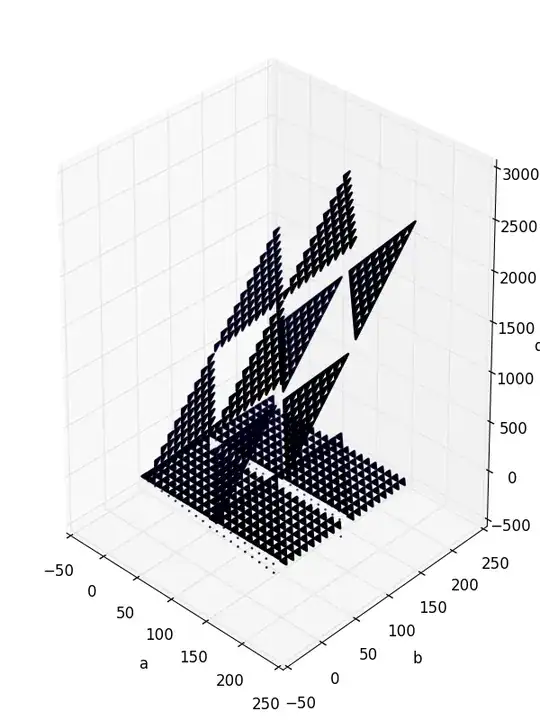
My question is: given $a, b$, how does $reverseadd(a, b)$ behave for larger values of $a$ and $b$, and how does it compare to $a+b$ (the original addition)? Given the examples in the linked question, there does not seem to be a correlation, since $reverseadd(22,58)=701$, whereas $reverseadd(73,33) = 7$.
I developed Python 3 code to return the reversed addition of $a, b$ (that may be useful for finding heuristics):
def r_add(a, b):
s_a = str(a)
s_b = str(b)
if len(s_a) < len(s_b):
s_a = s_a.zfill(len(s_b))
elif len(s_a) > len(s_b):
s_b = s_b.zfill(len(s_a))
# now same length
s_a = s_a[::-1]
s_b = s_b[::-1]
return int(str(int(s_a)+int(s_b))[::-1])
If you prefer to use another language, you can use some of the answers to the linked question.
Edit: after looking at values of $a, b \le 200$, there does seem to be a lot of cool symmetries: