This question is motivated by the first few explicit examples I came across, e.g.
Wikipedia, Inverse limit or this question or Wiki, Direct limit
In order to answer that question, let's start with the following two examples and an attempt to link the pullback and pushforward to the product and coproduct respectively. In the category $ \mathbf{Set} $ with monomorphisms only as arrows, these correspond respectively to the intersection and union:
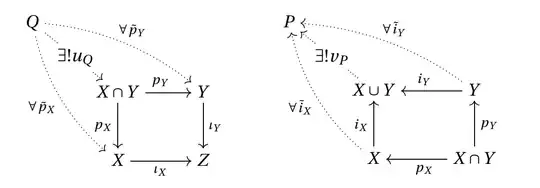
The explicit (and seemingly general) constructed goes like $$ X\cap Y:= \left\{(x,y)\in X\times Y,\ \iota_X(x) = \iota_Y (y) \right\}$$ where $p_{X/Y}$ are the projections on the first (resp. second) element in the pair $(x,y)$. (This construction actually corresponds to $\Delta(X\cap Y)\subset Z\times Z$ where $\Delta$ is the "diagonal map") and $$ X\cup Y:= X\coprod Y \Bigg/\sim$$ where $\sim$ is the finest equivalence relation such that $$ u\sim v ,\enspace u,v\in X\coprod Y \quad \Longleftrightarrow\quad u=i_X\circ p_X (x,y),\ v=i_Y\circ p_Y (x,y)\ \text{for some}\ (x,y)\in X\cap Y$$
(The attemp to relate intersection-product and union-coprodut by inserting $Q:= X\times Y$ or $P:= X\coprod Y$ in their respective diagrams fails because these don't make the diagrams commute.)
However, one can insert $C:= X\cap Y,\ f/g = p_X/p_Y$ in the following product diagram and $D:= X\cup Y,\ h/l =i_X/i_Y$ in the coproduct diagram:
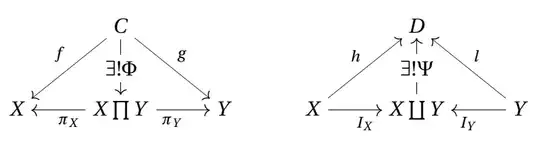
This gives a maps $\Phi : X\cap Y \rightarrow X\times Y$ and $\Psi: X\coprod Y \rightarrow X\cup Y$. The question can now be formulated as: under what condition are $\Psi,\Phi$ respectively monomorphism, epimorphism?
Same question for more general projective limits and inductive limits.
Remark: In e.g. this post, people emphasized that the diagrams correspond to the set construction only in $\mathbf{Set}$ with monomorphisms as arrows, not will all arrows, so that $\Psi$ is naturally a monomorphism, i.e. $X\cap Y$ a subobject of $X\times Y$.
Feel free to add the relevant tags.