What fraction of a sphere can an external observer see?

Question

Here is a geometry problem.

1. Let there be a ball of radius R and let's call it the Moon.
2. Let there be an external observer: A.
3. A is at a distance d to (the surface of) the Moon.
4. [Edit] A is a Cyclope, he has only one eye.

Question:

What fraction of the sphere can A see?

I would like the solution with a demonstration.

Thank you.

Answer 1

Take a plane through $A$ and the centre of the sphere, $C$. Construct the two tangents to the sphere from $A$, and say that one of them meets the sphere at $B$. Now find the angle, $\theta = \angle ACB$, that the radius through $B$, $CB$ (which is perpendicular to the tangent, of course) makes with the radial line $CA$: consider the triangle $ABC$. Then you know the radius of the sphere is $R$, and that's the adjacent side, and the distance to the centre from $A$ is $R+d$, so that's the hypotenuse. Hence $$ \cos{\theta} = \frac{R}{R+d} = \frac{1}{1+d/R}. $$

Now, the formula for the area of a spherical cap is $$ 2\pi R^2(1-\cos{\theta}), $$ so the total area is $$ 2\pi R^2 \left( 1-\frac{1}{1+d/R} \right) $$ and the fraction of the total area is $$ \frac{1}{4\pi R^2} 2\pi R^2 \left( 1-\frac{1}{1+d/R} \right) = \frac{d}{2(R+d)}. $$

Answer 2

Since, $d$ is the distance of the observer's eye from the surface hence the distance of the observer's eye from the center of the moon is $R+d$. (As shown in the figure below, observer's eye (at the point $O$) is at a distance $(d+R)$ from the center $C$ of the sphere (Moon))

Now, let $2\alpha$ be the cone angle subtended by the surface visible to the observer & draw any tangent line to the surface (of moon) to obtain a right triangle in which we have $$\cos \alpha=\frac{\text{radius}}{\text{distance from the center}}$$ $$\color{blue}{\cos \alpha=\frac{R}{R+d}}$$
Now, consider an elementary (circular) ring of width $Rd\theta$ & radius $R\sin\theta$ (area $(Rd\theta)(2\pi R \sin\theta$) on the spherical surface then the $\color{blue}{\text{area visible to the observer}}$ (Using integration ) $$=\int_{0}^{\alpha} (R d\theta)(2\pi R\sin \theta) $$ $$=2\pi R^2\int_{0}^{\alpha}\sin\theta d\theta$$ $$=2\pi R^2\left[-\cos\theta\right]_{0}^{\alpha}=2\pi R^2\left[-\cos\alpha+1\right]$$$$=2\pi R^2 (1-\cos \alpha)$$ $$=2\pi R^2 \left(1-\frac{R}{R+d}\right)$$ $$=2\pi R^2 \left(\frac{d}{R+d}\right)$$

Hence, the $\color{blue}{\text{fraction of surface area visible to the observer}}$ $$=\frac{\text{area visible to the observer}}{\text{total surface area}}$$ $$=\frac{2\pi R^2 \left(\frac{d}{R+d}\right)}{4\pi R^2}$$ $$\color{blue}{=\frac{d}{2(R+d)}}$$

Answer 3

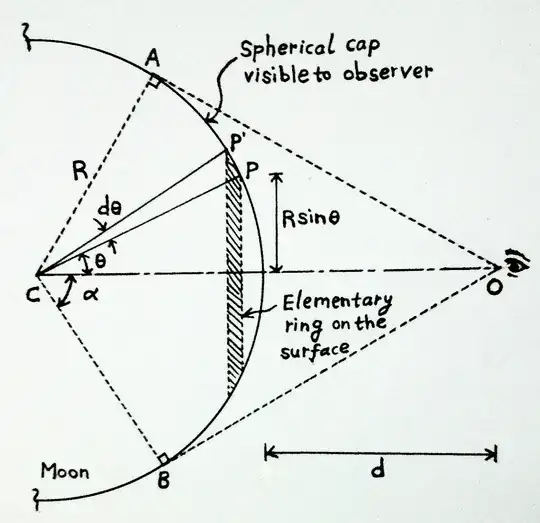
Let's assume you're looking from above, so that you see a region of the sphere that looks like the arctic --everything above some latitude line $y = c$ (which constitutes a circle on the sphere itself). The area of this "cap" region is $2\pi R (R - c)$ (See below).

So the only question is "what's $c$?" From the earth's center to the eye to a point on the circle-of-latitude is a right triangle; the short leg is $R$, the hypotenuse is $R + d$, so the long leg is $$ a = \sqrt{ (R+d)^2 - R^2 } $$

The angle at the earth's center is then $\theta = \arccos(\frac{R}{R+d})$, so the $y$-coordinate of the latitude line is $R$ times the cosine of that angle, i.e., $$ c = R\cos\left(\arccos\frac R{R+d}\right) = \frac{R^2}{R+d}, $$ and the area is \begin{align} 2\pi R (R - c) &= 2\pi R \left(R - \frac{R^2}{R+d}\right) \\ &= 2\pi R\frac{R(R+d)-R^2}{R+d}\\ &= 2\pi R\frac{Rd}{R+d}\\ &= 2\pi R^2\frac d{R+d}\\ \end{align}

Reason for the area claim above: the map that projects a point $(x, y, z)$ of a sphere to the point $(x/R, y, z/R)$ of the circumscribed cylinder, where $R = \sqrt{x^2 + z^2}$, has a derivative whose determinant is 1, so it's area preserving. So the area of a cap of the sphere above height $c$ is the same as the area of a slice of a cylinder above height $c$, namely $2\pi R (R - c)$.

Answer 4

Here’s an entirely different approach, certainly not what you asked for.

The answer is quite easy once you know the formula for the area of a spherical cap (the area inside a small circle {*}). If the angular radius of your cap is $\theta$, then the area inside is $2\pi(1-\cos\theta)R^2$. To tell the truth, I’m too lazy to write out the proof, which involves an easy integration, so I’ll skip it. Anyway, when you divide this by the area of the whole sphere ($4\pi R^2$), you get $(1-\cos\theta)/2$.

As John Hughes says in his answer, you’re dealing with a right triangle, and you see, by making a planar cross-section, that if the Moon subtends an angle of $2\varphi$ as you observe it, the angular radius $\theta$ of your cap is the complement of $\varphi$. Since the Moon, from the Earth, subtends an angle of about $1/2^\circ$, $\theta=89.75^\circ$. And when you plug this into the formula, you get $49.782\%\,$. (If the Moon had been spherical, which it definitely isn’t.)

{*} a small circle is a circle on the surface of the sphere that is (usually) not a great circle.

Answer 5

Some already known geometric properties can be used.

Upto point of tangency, distance along axis is harmonic mean of extremes ( a property at tangency), between $ d , ( 2 R +d ) = \frac {d (2R+d)}{R+d} $.

Subtracting d, we get $ \frac {R d}{R+d} $ as the height $h$ of spherical cap.

Using property that surface of area of spherical segment is proportional to cap segment height [ $ (h/2R) * 4 \pi R^2 $ ], we divide the above by $2 R $ to get $ \dfrac {d}{2(R+d)}. $