7

Find the number of positive integers solutions of the equation $3x+2y=37$ where $x>0,y>0,\ \ x,y\in \mathbb{Z}$ .

By trial and error I found

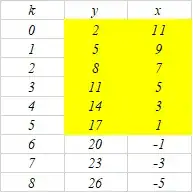
$$\begin{array}{|c|c|} \hline x & y \\ \hline 11 & 2 \\ \hline 9 & 5 \\ \hline 7 & 8 \\ \hline 5 & 11 \\ \hline 3 & 14 \\ \hline 1 & 17 \\ \hline \end{array}$$

Total $\large 6$ pair of solutions. But i would like to know if their is a specific method to only find the number of positive solutions and not necessarily the actual solutions.

I look for a short and simple way. I have studied maths upto $12th$ grade.

Bart Michels
  • 26,985
  • 6
  • 59
  • 123
R K
  • 3,035

6 Answers6

7

In the world of combinatorics, you can use something commonly known as the "stars and bars" method. Generally put, the equation $$x_1+x_2+\ldots+ x_k = s$$ where $s,x_i$ are positive integers has $\binom{s-1}{k-1}$ many solutions. The quantity $\binom{s-1}{k-1}$ is called a binomial coefficient. A general binomial coefficient $\binom{a}{b}$ where $a,b$ are nonnegative integers with $a \geq b$ is defined as $$\binom{a}{b} =\frac{a!}{b!(a-b)!}$$ which means $$ \binom{s-1}{k-1} = \frac{(s-1)!}{(k-1)!(s-k)!}$$ In your problem we have $s = 37$ and $k = 2$. So, we want to calculate $$\binom{37-1}{2-1} = \frac{36!}{1!\space 35!} = 36$$ However, this tells us that the equation $x+y = 37$ has $36$ solutions. Since your equation is $3x+2y = 37$, we'll want every third $x$ and every second $y$. This is tantamount to dividing $36$ by $3$ and $2$. We get $\frac{36}{3\cdot 2} = 6$, which matches your calculation. (Had the ratio not been an integer, you'd want to round down to the nearest integer). Depending on how large $k$ and $s$ are, you may find the stars and bars method to be preferable to calculating every solution by hand. It really boils down to a pretty easy factorial calculation. I'd say your problem could go either way.

graydad
  • 14,325
  • An elegant generalized answer! – Ataulfo Jun 04 '15 at 18:51
  • The equation $x+y=8$ has $7$ solutions. According to your argument the equation $3x+2y=8$ would have ${7\over6}$ solutions. – Christian Blatter Jun 04 '15 at 19:22
  • @ChristianBlatter see my comment in parentheses about rounding down to the nearest integer – graydad Jun 04 '15 at 19:29
  • @graydad: how would u define in the decimal numbers like $2.5 ,\ \ 1.5$ would they be considered as $3,\ \ 2$ or $2,\ \ 1$ – R K Jun 04 '15 at 19:48
  • @RK Do you have a little more context? If you are talking about the $\frac{\text{Total Solutions}}{\text{Product of coefficients}}$ part in my answer, notice I say that you should round down to the nearest integer if you get a non integer answer. – graydad Jun 04 '15 at 19:49
  • i mean in the parenthesis as u wrote if the ratio of the integers came as $2.5 $ or $1.5$ then will they be considered as $3$ or $2$ , otherwise $2$ or $1$ . – R K Jun 04 '15 at 19:51
  • @RK You round down those numbers to the largest integer less than $2.5$ and $1.5$. That would get you $2$ and $1$ respectively. – graydad Jun 04 '15 at 19:52
  • $\quad$ ohk thanks. – R K Jun 04 '15 at 19:54
  • 3
    The equation $x+y=5$ has $4$ positive integral solutions. According to your argument the equation $3x+2y=5$ would have $[4/6]=0$ solutions. However one can check that $(1,1)$ is a solution. – Antoine Sep 22 '16 at 17:25
  • The number of solutions of $ax+by=c$ with $\gcd(a,b)=1$ is not typically, for fixed $a,b,$ weakly monotone increasing with $c,$ so no formula based on stars and bars, by adjusting by division by $ab$ [or any related constant] and then taking floor or ceiling, can be right, since a formula of the latter type is weakly increasing with $c.$ – coffeemath Nov 17 '18 at 19:19
1

Take any of your six positive solutions, say the first one $(11, 2)$; you have $3\cdot11 +2\cdot2 = 37$ and for another solution $(x, y)$ you have $3x +2y = 37$.

Hence $3(x-11)+2(y-2)=0$ and all the solutions are given by $(x, y) = (11 +2t, 2-3t)$. Do you want $11 + 2t \gt 0$ and $2 - 3t \gt 0$ therefore $-5.5 \lt t \lt 1$.

Thus the only positive integer solutions correspond to the parameter $t = -5, -4, -3, -2 , -1, 0$ exactly the six ones you have found.

Alex M.
  • 35,927
Ataulfo
  • 32,657
0

Once you have found a duet of numbers $(x,y)$ satisfying this equation, let consider another duet as $$ (x_1=x+a, y_1=y-b) $$ For this second duet to satisfy the same equation, it is needed that

$$ 3a-2b=0 $$

Which leads to all the possible duets written as $$ (x+2n, y-3n) $$ With $n$ in $\mathbb{N}$.

Aulo
  • 51
0

By Hit and trial find one pair by putting the minimum value of either x or y.

3x+2y=37

let's assume x=1 ==> y=(37-3)/2 We got one pair (x,y) = (1,17)

Now, sum up the received pair by adding interchanging coefficients:

Here Y value is greater so we will apply by adding the opposite coefficients using the (+,-) operation. We can use (-,+) operation as well if the value of x is greater than y.

(1 + (co-efficient of y) , 17 - (co-efficient of x))

Other Pair : (1+2,17-3) ==> (3,14)

Next Pair : (3+2, 14-3) ==> (5,11)

Likewise, continue until any of the x or y reaches near 0

Last Pair : (11,2)

Pairs: (1,17), (3, 14), (5, 11), (7,8), (9, 5), (11, 2)

Total Number of Integral Solutions : 6

In this way, we can obtain all integral solutions of any given equation within few seconds.

Ketul Chhaya
  • 1
0
  1. Due to $gcd(3,2)=1$, so equation $3x+2y=37$ has solution, solve the equation we get $y=3k+2,~x=-2k+11, k∈N ⟹ 3k+2≥0 ~and ~-2k+11≥0, hence ~0≤k≤5 $, becasuse $k$ is integer, so $k=0,1,2,3,4,5$, so that we know the solutions pairs $(x,y)$ are 6. You can easy test such as well.

enter image description here

  1. How to solve equation $3x+2y=37$? We can use undetermined coefficient method find a particular solution to such linear Diophantine equation:

Let $y=3k+a ~ ⟹~ 3x+2(3k+a)=37~$ ⟹ $~ x= -2k+12+(1-2a)/3$, when $a=2 ~ $ then $~ x$ is integer , so that $x=-2k+11,y=3k+2, ~ k∈N$.

xMath
  • 95
-1

Considering: 3x + 2y = 37
It will have: Floor(Floor(37/3)/2)=6 positive integer solutions Consider: 2y = 37-3x The max number of possible solutions is < Floor(37/3)=12 That is: {1, 2, 3, ..., 12} are the possible solutions But: 37-3x (mod 2) = 0 (as 2 must divide 37-3x)

So generally: ax + 2y = c Will have Floor(Floor(c/a)/2) positive integer solutions

Jud Imhoff
  • 1