4

This question was inspired by this Quora question.

I'm sure lots of you are familiar with the fact that we have many different representations of $\pi$, things like $$ \begin{align} \pi & = \sqrt{6\zeta(2)} \\ & = \frac{4}{1 + \frac{1^2}{3 + \frac{2^2}{5 + \frac{3^2}{7 + \frac{4^2}{9 + \ddots}}}}} \\ & = 2\frac{2}{\sqrt{2}}\frac{2}{\sqrt{2 + \sqrt{2}}}\frac{2}{\sqrt{2+\sqrt{2+\sqrt{2}}}}\cdots \\ & = \frac{9801}{2\sqrt{2}}\left(\sum_{k=0}^\infty{\frac{(4k)!(1103 + 26390k)}{k!^4(396^{4k})}}\right)^{-1} \\ & = \frac{640320^{3/2}}{12}\left(\sum_{k=0}^\infty{\frac{(6k)!(13591409 + 545140134k)}{(3k)!(k!)^3(-640320)^{3k}}}\right)^{-1} \\ & = \lim_{r\to\infty}\frac{1}{r^2}\sum_{x=-r}^r\sum_{y=-r}^r{\left[\sqrt{x^2+y^2}\le r\right]} \\ & = \frac{2}{\operatorname{Li}_2(3-\sqrt{8})-\operatorname{Li}_2(\sqrt{8}-3)}\int_0^1{\frac{\arctan^2x}{\sqrt{1-x^2}}\text{d}x} \\ & = \left(\Gamma\left(\frac34\right)\sum_{n\in\Bbb{Z}}e^{-\pi n^2}\right)^4 \\ & = \cdots \end{align} $$ and the list continues indefinitely.

All of these, obviously, have their respective individual proofs. Some proofs rely on one another, others stem from thinking about $\pi$ in a fundamentally new way (such as 6th identity, which is basically a mathematical encoding of the number of points inside the unit circle in a square region), and others are results obtained in reverse (such as the last two identities).

What interests me is not how each one of these proofs is carried out independently, it's how they are associated that interests me. My question is this; how "independent" are two proofs? Another way of stating this problem might be, for any two identities with different proofs (i.e. any two proofs of a formula for $\pi$), can you go directly from one identity to the other without passing through the original identity?

Let me see if I can describe this better. I'm sorry I don't have the background on proof theory or logic theory or things like that necessary to make the semantics of my question well defined, but I'll do my best to give a notion of what "independence" means in regards to two proofs.

Say we wanted to show for example, that $$ 2\frac{2}{\sqrt{2}}\frac{2}{\sqrt{2 + \sqrt{2}}}\frac{2}{\sqrt{2+\sqrt{2+\sqrt{2}}}}\cdots = \frac{2}{\operatorname{Li}_2(3-\sqrt{8})-\operatorname{Li}_2(\sqrt{8}-3)}\int_0^1{\frac{\arctan^2x}{\sqrt{1-x^2}}\text{d}x} $$ Would there be a way of proving that this is true without just proving that both sides are equal to $\pi$?

So in general, say we have two formulas $\mathbf{A}$ and $\mathbf{B}$ that both evaluate to the same constant $c$. That is $$ \mathbf{A} = c, \qquad \mathbf{B} = c $$ and thus $$ \mathbf{A} = \mathbf{B} $$ because $c = c$. If we weren't allowed to use the fact that both $\mathbf{A}$ and $\mathbf{B}$ are equal to $c$, is there always a way to prove $\mathbf{A} = \mathbf{B}$? In my head it looks like this:

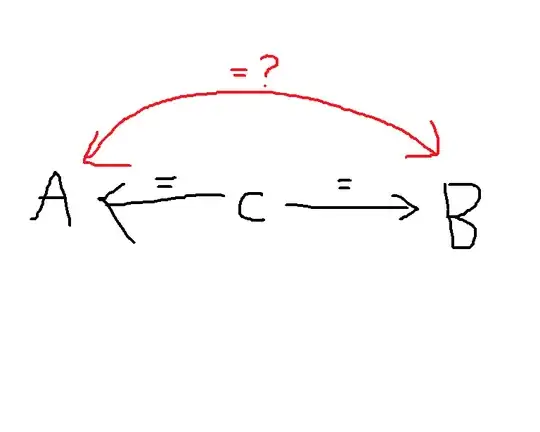
enter image description here

Can we always find the red line that proves $\mathbf{A}$ and $\mathbf{B}$ are equal without going through any of the black lines?

In addition, if this question isn't very well understood yet, are there any interesting advances in proof theory or other disciplines that have gotten us any closer? What literature is there on this topic?

user3002473
  • 9,245
  • 2
    I'm not sure your notion is well-defined. May we use $A+1=c+1$ and $c+1=B+1$? How about $2A=2c$ and $2c=2B$? While these results may seem like "trivial" variations of your forbidden results, I suspect that it would be difficult to impossible to formalize this notion of "trivial variants". – Zach Effman Jun 04 '15 at 01:54
  • @ZachEffman I understand what you mean, that's why I'm having such a difficult time formulating this question. Would it be more well defined if I asked if it were possible to prove $A = B$ without knowing at all that $A = c$ and $B = c$ in the first place? – user3002473 Jun 04 '15 at 01:56
  • But if $A=c$ and $B=c$, you wouldn't have to know that these identities hold in the first place--you could prove them on the spot, glue the proofs together, and end up with a proof that $A=B$ without any 'prior knowledge'. – Zach Effman Jun 04 '15 at 01:59
  • 1
    I don't think the idea of prior knowledge is useful. More useful would be to ask for proof that never includes the strings $A=c$ or $B=c$, but then you'd have to exclude all the trivial variants of those strings, and that would require a definition of "trivial variant". I suspect that any reasonable definition would force all true identities to be trivial variants of each other – Zach Effman Jun 04 '15 at 02:00
  • Hmm, I think I see. Do you know of any literature that goes more in-depth on these topics that might help us get closer to a formal definition? – user3002473 Jun 04 '15 at 02:03
  • I'm sorry to say that I don't. It may well be that somebody else has come up with the right formalization, but I'm not familiar with it – Zach Effman Jun 04 '15 at 02:04
  • When I was an undergraduate I wanted to prove that $\sum_{n=1}^\infty \frac{1}{n^2}=\pi^2/6$. Not having a lot of background at the time, I thought maybe one could somehow derive it from the Leibniz series $\sum_{n=1}^\infty \frac{(-1)^{n-1}}{n}=\pi/4$, but I never was able to get it to work. I have a feeling these two identities are independent in the sense you are trying to capture. – Cheerful Parsnip Aug 12 '16 at 15:45
  • I am not sure how this question should be tagged, but it is definitely not proof-verification. Not to mention that (proof-verification) should not be used as the only tag for a question. – Martin Sleziak Aug 18 '16 at 08:28
  • @MartinSleziak You're right, guess I overlooked that. How's "proof-theory" and "soft-question"? – user3002473 Aug 18 '16 at 12:41

0 Answers0