5

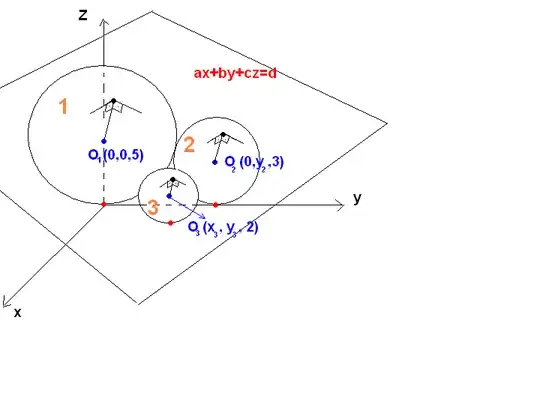
enter image description here

3 spheres are on $z=0$ plane and touch each other as shown in the picture. Coordinates of their centers are $O_1=(0,0,5),O_2=(0,y_2,3),O_3=(x_3,y_3,2)$. What is the tangent plane equation on 3 spheres? ($ax+by+cz=d$)

Thanks for answers.

Mathlover
  • 10,256
  • You're going to need to give the radii too... – Peter Taylor Apr 09 '12 at 20:34
  • The radii are already given by the coordiantes of the centres. Interesting question.... One thing to note is that $(a,b,c)$ is the normal vector to the plane $ax+by+cz=d$, so the problem might be simplified by trying to find the normal vector first. – William Apr 09 '12 at 20:35
  • 1
    Reminds me of this proof without words on MathOverflow. Which implies that if you extend a line passing through the centers of any two of the spheres, the point where it meets the $z=0$ plane must also lie on the desired plane. Not sure if that leads anywhere, but it's interesting. –  Apr 09 '12 at 20:46
  • @you, I missed the "touch each other". Thanks. – Peter Taylor Apr 10 '12 at 10:22

4 Answers4

4

First solve some quadratic equations to find $y_2$, $x_3$, and $y_3$.

Then, since each of the spheres is tangent to $z=0$ as well as to the mystery plane, its center must lie on the plane that bisects the angle made between these two planes. We can compute an equation for bisecting plane, because that is defined by the centers.

Now reflect the plane $z=0$ about the bisecting plane.

hmakholm left over Monica
  • 291,611
2

I get: -150.235 x-89.3299 y-128.83 z+1729.87=0 for the tangent plane equation. (Close approximation.)

Tangent points:

Sphere #1: {3.4594896600074643,2.05701926455194,7.966581035101458`}

Sphere #2: {2.0756918905582737,8.980177236680767,4.779953859745328`}

Sphere #3: {5.375454589335715,5.728584817849962,3.1866359029829208`}

Sphere center points:

Sphere #1 center point: {0, 0, 5}

Sphere #2 center point: {0., 7.74597, 3.}

Sphere #3 center point: {3.99166, 4.90578, 2.}

I calculated the tangent plane equation by using a plane thru 3 points. The first 2 points are apexes of 2 cones that envelope sphere #1 and sphere #2, then sphere #1 and sphere #3. Think of the line that connects the apexes as a hinge line that lies in the tangent plane. Select a third point whose x and y coordinates will be close to the tangent point on sphere #1. Reduce or add to the z coordinate as required to lower or raise the tangent plane. Plot each step as a visual aid. Using Mathematica, I used NMinimize to tell me how close the tangent plane was to sphere #1. When I was satisfied with the results, I took the coordinates as the tangent point. Repeat this with the other 2 sphere equations and the tangent plane equation to obtain the other 2 tangent points.

Regards,

Bill W.

Bill W.
  • 31
2

There are three methods to get direct solutions without iteration.

  1. Use an extended version of Gaussian elimination the results in having to get the fourth root of an equation. This technique is a general solution for geometry problems, with only the equations changed for this problem. You can use the symmetry of the plane-sphere tangent equations to make all but one row linear. The other rows break down to just two variables and a constant. You can then replace one of these with the other and a constant in the nonlinear. You end up with one variable in the for AX^4 +BX^3+CX^2+DX+E=0

  2. Another general solution that works. Expand the three spheres until two touch. Consider an inversion sphere where the spheres meet. (I like radius 1.0 since it allows the largest range of inversion.) The two spheres become two parallel planes. This gives you the the radius of the inverted solution and the midplane the center is on. Since you want a plane, the solution sphere must also go through the mirror point. Invert that sphere to get a plane and using the expansion coefficient to move the plane to the unexpanded tangency.

  3. Determine vectors from two centers to the center of the largest sphere. Scale (using the sphere radii) the vectors to determine two planes that slice that sphere. The intersection of that sphere and the two planes intersect where the plane is tangent. This gives you a vector from that center to that point that (when normalized) is the normal of the plane. Plugging the tangent point into the plane equation will generate the delta to complete the plane definition.

**I can give you the more details (and my solution) for any one of these if you post a request here. I do want to give a good answer, but each one takes time. **

  1. is dull but simple, except for the need for a quartic equation
  2. is a bit more interesting.
  3. is a bit more complex, but really interesting. It is a general solution for Appolonius' 10th problem in any number of (n) dimensions, as long as one of the tangent entities is a hypersphere. You need another, but simpler, method for a problem with all hyperplanes. You get the tangent plane by using the center of the inversion sphere as the (n+1)th tangency, which assures a plane.
John Fairman
  • 21
0

There is an exact solution using all closed form equations shown on the three attached pages. After the plane of symmetry through the three sphere's centers is defined, the lower tangent plane z=0 is mirrored across the plane of symmetry. To make the final solution clear, it's a plane fact that making d=1 in the plane's equation is the most useful convention (i.e. divide all ax+by+cz=d equation coefficients by 'd').
•Solution for equation of upper tangent plane is
(0.08792312)x + (0.05167692)y + (0.07399755)z = 1.0 ....or any multiple thereof.
•Sphere centers and tangent points (x,y,z) are
O1: (0.000, 0.000, 5.000); tangent point: (3.48894479, 2.05063178, 7.93635379);
O2: (0.000, 7.740, 3.000); tangent point: (2.09336687, 8.97077777, 4.76181227);
O3: (3.965, 4.865, 2.000); tangent point: (5.36027469, 5.68531592, 3.17454152)
•Here's how (actual calculations shown on the 3 images linked at the end):
1. First, the sphere centers' coordinates are easy to find using trigonometry. The Law of Cosines is used in this effort.
2. Those three center points' coordinates are used to define a plane that is a plane of symmetry of the 3-sphere group.
3. The normal vector perpendicular to this plane is defined as a unit normal vector.
4. The equation for the plane of symmetry is determined using the unit normal vector and the point at any of the spheres center's coordinates.
5. The tangent points of the tangent plane z=0 at the bottom of the spheres are defined.
6. The distance to the plane of symmetry of the tangent points at z=0 are found using vector analysis.
7. The bottom tangent points at z=0 are mirrored across the plane of symmetry using twice their distance from the plane of symmetry in the plane's normal vector direction.
8. The three new upper tangent points from step 7 are used to define the equation for the upper tangent plane. Calculations page 1 of 3 Calculations page 2 of 3 Calculations page 3 of 3

Ronald Crowell
  • 1