13

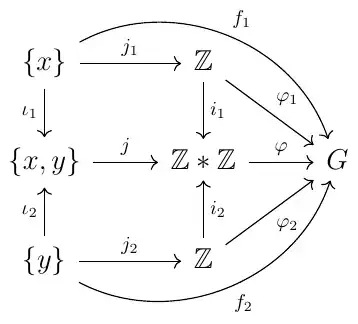
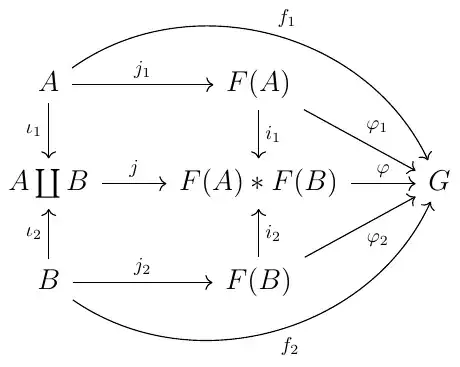
I want to show that the free group on two elements $F(\{x,y\})$ is the coproduct $\mathbb{Z}*\mathbb{Z}$ in $\textbf{Grp}$. The idea is to use the universal property of free groups to prove that $F(\{x,y\})$ satisfies the universal property of coproducts in $\textbf{Grp}$. Below is my attempt to prove this. Is this correct? and also I am having trouble extending this result to the free group on $n$ elements. Any help/comments will be appreciated. Thanks

Let $G$ be any group. Define $\gamma:\{x,y\}\rightarrow \mathbb{Z}$ to be the set map which send $x$ to the generator $1$ and $y$ to the identity. For the means of set up, let $J:\{x,y\}\rightarrow F(\{x,y\})$ be the set map native to the free group. Next denote $\iota:\mathbb{Z}\rightarrow F(\{x,y\})$ to be the inclusion map, which sends $1$ to the generator $x$. Now consider what we've established thus far

enter image description here

Now suppose that we have a group homomorphism $f:\mathbb{Z} \rightarrow G$, then $f\circ \gamma$ is a set map from $\{x,y\}$ and thus by the universal property of free groups there exists a unique group homomorphism $\phi:F(\{x,y\})\rightarrow G$ such that

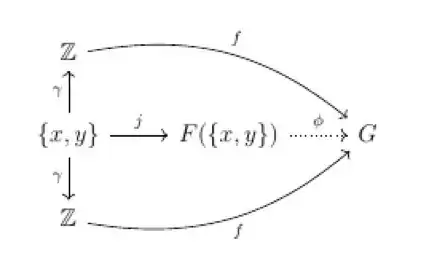
enter image description here

commutes. Now to show that $F(\{x,y\})$ is the coproduct $\mathbb{Z}*\mathbb{Z}$ in $\textbf{Grp}$, we must show that $f=\phi\circ\iota$, that is the following diagram commutes

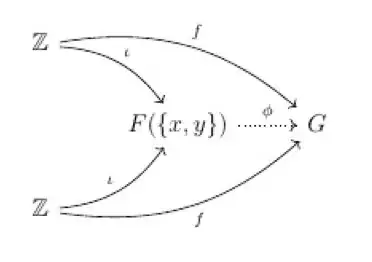
enter image description here

I claim that indeed it does. From the commutativity of the second diagram, we have that $f\circ\gamma=\phi\circ j$. It follows that $$f\circ\gamma(x)=f(1)=\phi(x)=\phi\circ j(x) \text{ and } f\circ\phi(y)=f(0)=\phi(y)=\phi\circ j(y)=e_G $$

Notice that $\phi\circ\iota(1)=\phi(x)=f(1)$, which shows that the homomorphism $\phi\circ\iota$ and $f$ agree for the generator of $\mathbb{Z}$ and so $\phi\circ\iota=f$ The commutativity of the third diagram is confirmed, proving that $F(\{x,y\})$ is the coproduct $\mathbb{Z}*\mathbb{Z}$ (we already have existence $\phi$ from the universal property of free groups, but not the uniqueness in this scenario?).

Martin Sleziak
  • 56,060
MAM
  • 798

3 Answers3

7

You're working too hard. I'll assume you're convinced that $\mathbb{Z}$ is the free group on one generator, which means you're convinced that

$$\text{Hom}(\mathbb{Z}, G) \cong G$$

(where the RHS should really be the underlying set of $G$ but I'm omitting that I'm applying the underlying set functor). One way to state the universal property of the coproduct is that

$$\text{Hom}(X \sqcup Y, Z) \cong \text{Hom}(X, Z) \times \text{Hom}(Y, Z)$$

from which it follows that

$$\text{Hom}(\mathbb{Z} \sqcup \mathbb{Z}, G) \cong G \times G$$

and this is also the universal property of the free group on two generators, so you're done by the Yoneda lemma. The argument is exactly the same for the free group on $n$ generators, and in fact on a set's worth of generators.

More abstractly, the forgetful functor $\text{Grp} \to \text{Set}$ has a left adjoint, the free group functor. As a left adjoint, it preserves colimits, and in particular coproducts. But every set $X$ is the coproduct of $X$ copies of the $1$-element set, so it follows that the free group $F_X$ is the coproduct of $X$ copies of $\mathbb{Z}$.

Qiaochu Yuan
  • 468,795
  • This problem is from Aluffi's Algebra Chapter 0 and not must category theory has been established at this point (no Yoneda lemma, no adjuncts,etc.).You were correct in assuming that I thought $F({x})\cong\mathbb{Z}$. Is it not, or is this a bad approach to take? Thanks – MAM May 20 '15 at 18:15
  • 2
    @MAM: wherever the problem comes from, you're going to learn the Yoneda lemma eventually, so you might as well learn it now. It is extremely useful in arguments like this: it implies that to show that two objects are isomorphic it suffices to show that they have the same universal property, and thinking that way makes the argument straightforward (and didn't require me to write down any commutative diagrams or anything). And yes, $\mathbb{Z}$ is the free group on one generator, and I use that fact above. – Qiaochu Yuan May 20 '15 at 18:49
  • Thanks for the response! How exactly are you using the Yoneda lemma? Are you using the embedding $y:\textbf{Grp}\rightarrow\textbf{set}^{\textbf{Grp}^{op}}$ given by $G\mapsto Hom(G,-)$, along with the fact that for groups $H$ and $K$, $H\cong K$ iff $yH\cong yK$? So in our case, showing $\text{Hom}(\mathbb{Z}\mathbb{Z},-)\cong \text{Hom}(F({a,b}),-)$ implies that $F({a,b})\cong \mathbb{Z}\mathbb{Z}$. – MAM May 26 '15 at 07:35
  • @MAM: yes, I'm using that if $\text{Hom}(H, -) \cong \text{Hom}(K, -)$ then $H \cong K$; more conceptually, this says that two objects are isomorphic if they have the same universal property, which is exactly what the argument above shows. This is a very general and useful way to show that objects are isomorphic. – Qiaochu Yuan May 26 '15 at 07:37
1

I'm late to the party, but here are my two cents.

You can think backwards: to show that the coprocuct $\mathbb Z * \mathbb Z$ in $\mathrm{Grp}$ satisfies the universal property for the free group $F(\{x,y\})$.

Consider the following commutative (as will be shown later) diagram. two elements set

$(j_1, \mathbb Z), (j_2, \mathbb Z)$ are free groups. So for any set maps $f_1: \{x\} \to G$, $f_2: \{y\} \to G$ there exists unique group homomorphisms $\varphi_1, \varphi_2$ that make corresponding diagrams commutative (i.e. $f_1 = j_1 \varphi_1$, $f_2 = j_2 \varphi_2$).

$\{x,y\}$ is the disjunctive union of $\{x\}$ and $\{y\}$. Let $\iota_1, \iota_2$ be corresponding canonical injections. Maps $f_1, f_2$ uniquely define the set map $f: \{x, y\} \to G$ (not shown on the diagram) such that $f_1 = f \iota_1$, $f_2 = f \iota_2$ due to the coproduct property of the disjoint union (or just obvious anyway). Any map $f: \{x,y\} \to G$ can be obtained this way.

Now groups coproduct joins the party. Let $i_1, i_2$ be morphisms of the coproduct. Then $\varphi_1$ and $\varphi_2$ define the unique group homomorphism $\varphi$ which makes triangles on the diagram commutative (i.e. $\varphi_1 = \varphi i_1$, $\varphi_2 = \varphi i_2$).

Due to the coproduct property of $\{x,y\}$, set maps $i_1 j_1: \{x\} \to \mathbb Z * \mathbb Z$ and $i_2 j_2 \{y\} \to \mathbb Z * \mathbb Z$ define the unique set map $j: \{x,y\} \to \mathbb Z * \mathbb Z$ which makes squares on the diagram commutative (i.e. $j \iota_1 = i_1 j_1$, $j \iota_2 = i_2 j_2$).

Let us show that $f = \varphi j$. One one hand $f_1 = f \iota_1$. On the other hand $f_1 = \varphi_1 j_1 = \varphi i_1 j_1 = \varphi j \iota_1$. So $f|_{\mathrm{im\,} \iota_1} = (\varphi j)|_{\mathrm{im\,} \iota_1}$. Analogously we get $f|_{\mathrm{im\,} \iota_2} = (\varphi j)|_{\mathrm{im\,} \iota_2}$. But $\{x,y\} = \mathrm{im\,} \iota_1 \coprod \mathrm{im\,} \iota_2$. So we conclude that $f = \varphi j$.

That means that $(j, \mathbb Z * \mathbb Z)$ satisfies the universal property for the free group $F(\{x,y\})$.

Analogously (almost verbatim) one can show that $F(A)*F(B)$ satisfies the universal property for the free group $F(A \coprod B)$ and thus $F(A \coprod B) = F(A)*F(B)$. two sets

vanger
  • 505
  • 1
    Every solution which is more than one line gives the impression that this result is non-trivial. I would advice against posting such solutions. – Martin Brandenburg Jul 13 '21 at 14:10
  • It still simpler than Qiaochu Yuan's solution that uses the Yoneda lemma. But I'm agree that that direction is more cumbersome than to show that $F(A \coprod B)$ satisfies the universal property for the coproduct. – vanger Jul 13 '21 at 20:54
  • You argue that a solution is simpler when it avoids the Yoneda Lemma? Everytime one avoids the Yoneda Lemma one actually reproves it in a special case. – Martin Brandenburg Jul 13 '21 at 21:04
  • Yes, because it's a homework question from the book. And when this exercise appeared, Yoneda lemma is not yet known. – vanger Jul 13 '21 at 21:12
  • This is a good answer given the context of the question. OP is working through Aluffi, who seems to want the student to work through a special case of Yoneda's lemma in order to gain footing in categorical arguments. Later in the book he addresses the Yoneda lemma (with an exercise) and shows its power in simplifying similar arguments. – Lepidopterist Feb 16 '25 at 20:07
0

I am also working through the Aluffi book, and came up with an explicit way (i.e. functions are defined explicitly) to show that the free group of set A={x, y} is a coproduct Z*Z in Grp (sorry for the bad notation)

Starting from Aluffi's hint, we know that F(A) is already an initial object in category F^A. That means there is already a unique group homomorphism φ from F(A) to an arbitrary group G and function f (from A to G), for an injection j (from A to F(A)). Moreover, explicitly:

j(x)=(0,0), j(y)=(1,1);

f(x)=e, f(y)=g

Thus, as you can verify, φ is well defined, unique and a group homomorphism.

Now suppose we have group (Z,+) and two functions i and i' from Z to A as follows:

i(0)=x, i(k)=y for all k≠0;

i'(0)=y, i'(k)=x for all k≠0

Then, verify that the diagram of F(A) as coproduct in Grp commutes, i.e.

f○i=φ○(j○i), f○i'=φ○(j○i')

These will suffice, since the property of φ as a unique group homomorphism will extend to this case, proving that F(A) is the coproduct of Z in Grp.

Here are the diagrams:

https://i.sstatic.net/IEADp.jpg

I apologize for the notations. Please let me know if it is wrong. I am working through the book on my own so from time to time I make mistakes!

Sincerely,

Alex

Gladiator
  • 141
  • 1
    What does $(0,0)$ and $(1,1)$ mean? I don’t think you understand what the free product is; it’s not the direct sum/direct product. – Arturo Magidin Apr 01 '20 at 16:00