3

Suppose that $\delta(A, B) = \dfrac{|A \Delta B|}{|A \cup B|}$, where $\Delta$ represents symmetric difference. Then how does one prove the triangle inequality, viz that $\delta(A, B) + \delta(B, C) \ge \delta(A, C)$?

Ben
  • 161
  • 1
    This question is not well defined. Can you write down exactly what you mean in mathematical notation. – Tim Raczkowski May 17 '15 at 23:44
  • This should help: http://meta.math.stackexchange.com/questions/5020/mathjax-basic-tutorial-and-quick-reference – Tim Raczkowski May 17 '15 at 23:45
  • 1
    But... How is the "number of properties" defined? As of what you said, all you can say about it is that it's a function $p:\mathbb{R}\to\mathbb{N}^+$.

    Which is not much, actually.

     –  May 18 '15 at 00:28

1 Answers1

7

If I understand you correctly, the objects you are considering are finite sets and your dissimilarity function is defined as $d(A, B) = \frac{|A \ominus B|}{|A \cup B|}$, where $\ominus$ denotes the symmetric difference.

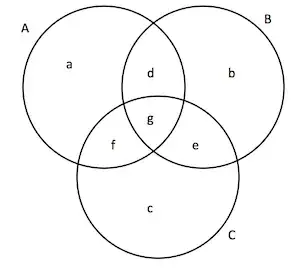
Consider the Venn diagram for three sets $A$, $B$, and $C$. Labelled Venn diagram

Then the triangle inequality boils down to $$ \frac{a+b+e+f}{a+b+d+e+f+g} + \frac{b+c+d+f}{b+c+d+e+f+g} \geq \frac{a+c+d+e}{a+c+d+e+f+g} $$

Plugging this into Wolfram Alpha, we see that it "simplifies" to: $$ \frac{a^2 b + a b^2 + a^2 c + 2 a b c + b^2 c + a c^2 + b c^2 + a^2 d + 2 a b d + b^2 d + 2 a c d + 2 b c d + a d^2 + b d^2 + 2 a b e + b^2 e + 2 a c e + 2 b c e + c^2 e + a d e + 2 b d e + c d e + b e^2 + c e^2 + a^2 f + 4 a b f + 2 b^2 f + 4 a c f + 4 b c f + c^2 f + 4 a d f + 5 b d f + 3 c d f + 2 d^2 f + 3 a e f + 5 b e f + 4 c e f + 4 d e f + 2 e^2 f + 3 a f^2 + 4 b f^2 + 3 c f^2 + 4 d f^2 + 4 e f^2 + 2 f^3 + 2 a b g + 2 b^2 g + 2 a c g + 2 b c g + a d g + 3 b d g + 3 b e g + c e g + 3 a f g + 6 b f g + 3 c f g + 4 d f g + 4 e f g + 4 f^2 g + 2 b g^2 + 2 f g^2}{(a + b + d + e + f + g) (a + c + d + e + f + g) (b + c + d + e + f + g)} \geq 0 $$

Since all the coefficients in the above expression are positive, and $a, b, c, d, e, f, g \geq 0$, we conclude that the inequality always holds.

augurar
  • 1,886
  • That's exactly the question I was trying to ask. But is there a simpler proof? – Ben May 18 '15 at 04:56
  • @Ben If possible, you should consider using the absolute number of differences, i.e. $|A\ominus B|$ without dividing by $|A\cup B|$. This can just be thought of as the $\ell_1$ norm on the Cartesian product of discrete metric spaces. – augurar May 18 '15 at 18:10
  • 1
    Thank you. I managed to find a complete version of this proof in Michael Levandowsky and David Winter (1971), "Distance Between Sets" Nature 234(5): 34-35. – Ben Jul 23 '15 at 08:55
  • Here is a more recent article, available from Reearchgate : "A note on the triangle inequality for the Jaccard distance" by Sven Kosub, Pattern Recognition Letters, Dec 2016. – Jean Marie Sep 17 '21 at 15:24
  • I would like to ask if this may be also applicable on "https://math.stackexchange.com/questions/4562107/triangular-inequality-and-metrics" . – Ricter Oct 27 '22 at 16:34