Tricky Rectangle Problem

Question

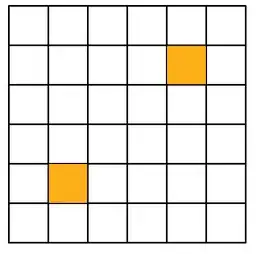
enter image description here

How many rectangles are there which do not include any yellow squares?

@Hippalectryon Counting by hand is not realistic since there are $\binom{7}{2}$ ways of selecting the horizontal sides and $\binom{7}{2}$ of selecting the vertical sides if we ignore the requirement that no yellow squares are selected. — N. F. Taussig, May 12 '15 at 20:19
@N.F.Taussig I was just trying to show that 'I haven't tried anything so far because I don't know how to start' showed a lack of effort. — Hippalectryon, May 12 '15 at 20:21
@N.F.Taussig: No counting by hand is realistic, because it forces one to take short-cuts when counting! Then the shortcuts become an answer! — user21820, May 13 '15 at 03:28

score 16 · Accepted Answer · 2015-05-12T20:41:28.460

16

Here is a more combinatorial/algebraic approach:

Let the Horizontal lines from bottom to top be $h_{0}, h_{1}, ..., h_{6}$ and Vertical lines from left to right be $v_{0}, v_{1}, ..., v_{6}$

Total Rectangles $= {7 \choose 2} \times {7 \choose 2} = 441$

Rectangles that contain bottom left yellow square is all rectangles that can be formed by choosing one horizontal line from $\{h_{0}, h_{1}\}$, another horizontal line from $\{h_{2}, ..., h_{6}\}$ and one vertical line from $\{v_{0}, v_{1}\}$, another vertical line from $\{v_{2}, ..., v_{6}\}$.

Total number of rectangles that contain bottom left yellow square $=$ $\left({2 \choose 1} \times {5 \choose 1} \right) \times \left({2 \choose 1} \times {5 \choose 1}\right) = 100$

Similarly, total number of rectangles that contain top right yellow square $=$ $\left({2 \choose 1} \times {5 \choose 1} \right) \times \left({2 \choose 1} \times {5 \choose 1}\right) = 100$

Total number of rectangles that contain both the yellow squares are all the rectangles that can be formed by choosing one horizontal line from $\{h_{0}, h_{1}\}$, another horizontal line from $\{h_{5}, h_{6}\}$ and one vertical line from $\{v_{0}, v_{1}\}$, another vertical line from $\{v_{5}, v_{6}\}$.

Total number of rectangles that contain both the yellow squares $=$ $\left({2 \choose 1} \times {2 \choose 1} \right) \times \left({2 \choose 1} \times {2 \choose 1}\right) = 16$

From principle of inclusion-exclusion: Rectangles without any yellow squares $=$ $441 - (100+100-16) = 257$

edited May 12 '15 at 20:41

answered May 12 '15 at 20:19

2

Wow, this is a quite solid proof in a very short time, bravo. – Atvin May 12 '15 at 20:22
1

It came in handy then, congrats. – Atvin May 12 '15 at 20:23
May I ask why the total rectangles is $^7C_2 \times ^7C_2$? – bnosnehpets May 12 '15 at 20:26
3

@bnosnehpets A rectangle is determined by its sides. There are seven vertical lines, from which we must choose two to form the vertical sides. Similarly, there are seven horizontal lines, from which we must choose two to form the horizontal sides. – N. F. Taussig May 12 '15 at 20:27
@mvw Basically $7C_2$ is the same as ${7 \choose 2}$ – May 12 '15 at 20:35
@N.F.Taussig Great explanation! – May 12 '15 at 20:36
@YagnaPatel I could say the same about your solution to this problem. Nice job. – N. F. Taussig May 12 '15 at 20:39
This is a very concise solution. – lauren May 12 '15 at 20:58
Any chance that the question, as stated, could be read to exclude counting "square" rectangles? – DJohnM May 12 '15 at 22:32
How come that my comment suggesting this approach has been deleted from the comments to the question? – Moti Mar 01 '21 at 04:25

Steven Alexis Gregory · Answer 2 · 2015-05-12T20:52:27.873

12

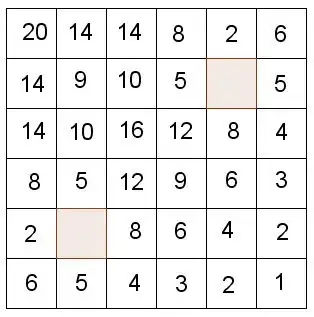
rectangle counter

What I did is, in each square, count the number of rectangles that could be drawn having the same upper left corner as that square, which also do not include the shaded squares I also got 257. I hope someone will check my work. I have a bit of a dyslexia - type problem and it's really hard for me to do things like this without messing up.

edited May 12 '15 at 20:52

answered May 12 '15 at 20:47

Steven Alexis Gregory

27,619

1

My row sums are: $64 + 43 + 64 + 43 + 22 + 21 = 257$ – mvw May 12 '15 at 20:52
@Steven Gregory: i like this proof. Very elegant. – David Quinn May 12 '15 at 21:15
@DavidQuinn: Thanks. I like that the sums are symmetrical about the diagonal. – Steven Alexis Gregory May 12 '15 at 21:25

mvw · Answer 3 · 2015-05-12T21:37:56.253

6

Here is an illustration to Yagna Patel's solution:

rectangles

Each possible rectangle is described by the choice of two horizontal and two vertical lines. This helps to emphasize the choice aspect. See e.g. the lower yellow rectangle $(h_1, h_2, v_1, v_2)$.

The lines can also be viewed as coordinate lines and we could say that rectangle has a lower left point $(1,1)$ and a higher right point $(2,2)$.

edited May 12 '15 at 21:37

answered May 12 '15 at 20:16

mvw

35,114

Nice, this is a great visual. – May 12 '15 at 21:18

Tricky Rectangle Problem

3 Answers3

Linked