I have an optimization problem of the form $$\operatorname*{argmax}_{\mathbf{w}} \sum_i \log(1 + \mathbf{w} \cdot \mathbf{k_i})$$ given some set of vectors, $\mathbf{ \{k_i\} }$. I have tried both gradient descent and BFGS, but both of them are slow. Is this a well known problem, and are there existing software implementations that can quickly solve a problem of this form?
Asked
Active
Viewed 95 times
1
-
$w,k_i\in \mathbb R^n$, what is $n$ and what range of $i$ ? – Nikita Evseev May 10 '15 at 06:44
-
Without more detail it is hard to answer, do the $k_i$ satisfy some condition that will ensure that a maximum exists? – copper.hat May 10 '15 at 07:19
-
1Did you try Newton's method (with a line search, of course)? Is it practical, given the size of the Hessian matrix or its structure? – Alex Shtoff May 10 '15 at 11:58
1 Answers
0
There must be some constraint on $\boldsymbol{w}$ and $\boldsymbol{k}_{i}$. Otherwise the problem is not well defined.
I found setting all vectors on the unit ball and forcing $\boldsymbol{w}$ to be within the unit ball to be sensible.
The problem becomes:
$$ \arg \min_{\boldsymbol{w}} - \sum_{i = 1}^{n} \log \left( 1 + \boldsymbol{w}^{T} \boldsymbol{k}_{i} \right), \; \text{ subject to } \; {\left\| \boldsymbol{w} \right\|}_{2} \leq 1 $$
Where $\forall i: \; {\left\| \boldsymbol{k}_{i} \right\|}_{2} = 1$.
One simple way to solve this is the projected gradient descent with the Orthogonal Projection onto the L2 Unit Ball.
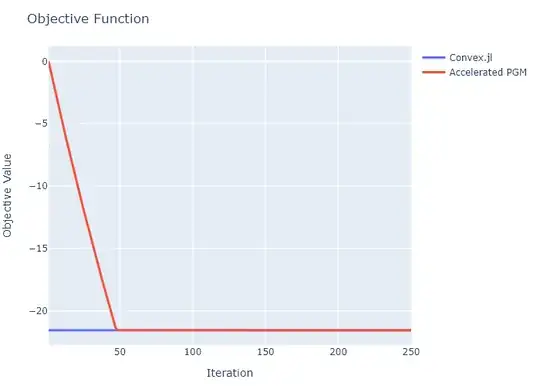
I compared the results with a DCP solver (Convex.jl):
In the case above $n = 500, m = 250$.
The convergence happens within 50 iterations.
An unoptimized Julia code runs 250 iterations in 7.6 [Mili Sec].
I consider that to be pretty fast.
The full code is available on my StackExchange Mathematics GitHub Repository (Look at the Mathematics\Q1275192 folder).
Royi
- 10,050