6

I'm trying to solve some problems in differential topology, and I came across the following: suppose $f:M\times [0,1]\rightarrow N$ is a homotopy, where $M$ is a compact manifold, such that $f_0$ and $f_1$ are $C^r$ functions, both transversal to a submanifold $K\subset N$, where $K$ is also compact; then there exists $W\subset M\times [0,1]$ a compact submanifold such that $\partial W=f^{-1}_0(K)\cup f_{1}^{-1}(K)$.

I know that one can assume that the homotopy is also a $C^r$-function (by Whitney Approximation Theorem) and, since both $f_0$ and $f_1$ are transversal to $K$, then $f^{-1}_0(K)$ and $f^{-1}_1(K)$ are submanifolds of $M$.

When we look at $M\times [0,1]$, the situation is the following: 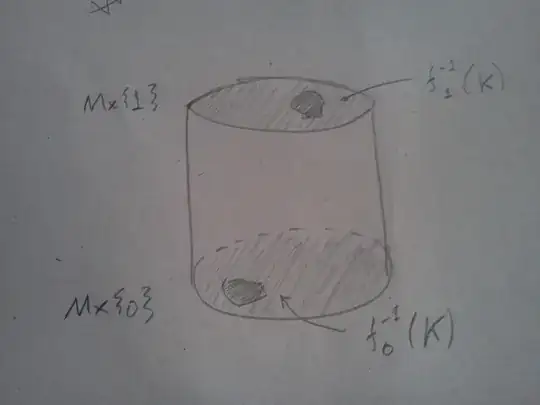enter image description here Besides it seems intuitively clear that we can "connect" $f^{-1}_0(K)$ to $f^{-1}_1(K)$, how this can be done formally?

Thank you

C. Falcon
  • 19,553
Pryscilla Silva
  • 843
  • Since you know that the homotopy $f$ can be chosen to be a smooth you could take $f^{-1}(K)\subset M\times [0,1]$, if $f$ were made transversal to $K$ I think you are done. Does it make sense? – Studzinski Apr 26 '15 at 15:19
  • I think it does make sense. But how to guarantee that $f$ is transversal do $K$? Or, more precisely, how to obtain an function $g$, homotopic to $f$, transversal to $K$ and such that $g_0=f_0$ and $g_1=f_1$? – Pryscilla Silva Apr 26 '15 at 15:50
  • 1
    It is a general theorem that if $A$ is a compact manifold with boundary, $f: A \to B$ a smooth map, $K \subset B$ a compact submanifold, then $f$ can be homotoped to be transverse to $K$. If $\partial f: \partial A \to B$ is already transverse to $K$, the homotopy can be chosen to not change $f$ on $\partial A$. You can find this in, e.g., Guillemin and Pollack's differential topology book. –  Apr 26 '15 at 18:21

0 Answers0