I am going to work out the analysis here in the answer, and see if I am able to make sense of your question in the process.
We are given the two parameter oscillator:
$$ \ddot{x} + ax + bx^3 = 0$$
We can rewrite this as follows:
$$
\begin{align}
\dot{x} &= y \\
\dot{y} & = -ax - b{x^3}
\end{align}
$$
I might refer to $\mathbf{f}(x, y) = (\dot{x}, \dot{y})$ later.
Fixed points occur when nullclines intersect. That is:
$$
\begin{align}
&\quad\; \dot{x} = 0 \wedge \dot{y} = 0 \\
&\equiv y = 0 \wedge 0 = -ax -bx^3 \\
&\equiv y = 0 \wedge 0 = x(-a - bx^2) \\
&\equiv y = 0 \wedge \left(x = 0 \vee x = \pm\sqrt{-a/b}\right) \\
&\equiv (y = 0 \wedge x = 0) \vee \left(y = 0 \wedge x = \sqrt{-a/b}\right) \vee \left(y = 0 \wedge x = -\sqrt{-a/b}\right)
\end{align}
$$
So, there are three fixed points. $\mathbf{p}_1^* = (0, 0)$ is independent of the parameters (i.e. exists for all values of the parameter). The other two ($\mathbf{p}_2^* = (\sqrt{-a/b}, 0)$ and $\mathbf{p}_3^* = (-\sqrt{-a/b}, 0)$) depend on the parameters. In particular, they only exist if $ab < 0$.
We can determine the topological type of hyperbolic fixed points using linear stability analysis. Consider the Jacobian of the problem at hand:
$$
\begin{align}
\mathbb{J}(\mathbf{f}) = \left[\begin{array}{cc} \partial\dot{x}/\partial x & \partial\dot{x}/\partial y \\ \partial\dot{y}/\partial x & \partial\dot{y}/\partial y \end{array}\right] = \left[\begin{array}{cc} 0 & 1 \\ -3bx^2 -a & 0 \end{array}\right]
\end{align}
$$
Call the determinant of the Jacobian $\Delta$. Call the trace of the Jacobian $\tau$. We can use $\Delta$ and $\tau$ to figure out the topological type of hyperbolic fixed points.
Let us evalulate the Jacobian at the fixed points. At $\mathbf{p}_1^*$:
$$
\begin{align}
\mathbb{J}(\mathbf{f})\mid_{(0, 0)} &= \left[\begin{array}{cc} 0 & 1 \\ -a & 0 \end{array}\right] \\
\Delta_1 &= a \\
\tau_1 &= 0
\end{align}
$$
At $\mathbf{p}_2^*$:
$$
\begin{align}
\mathbb{J}(\mathbf{f})\mid_{(\sqrt{-a/b}, 0)} &= \left[\begin{array}{cc} 0 & 1 \\ 2a & 0 \end{array}\right] \\
\Delta_2 &= -2a \\
\tau_2 &= 0
\end{align}
$$
At $\mathbf{p}_3^*$:
$$
\begin{align}
\mathbb{J}(\mathbf{f})\mid_{(-\sqrt{-a/b}, 0)} &= \left[\begin{array}{cc} 0 & 1 \\ 2a & 0 \end{array}\right] \\
\Delta_3 &= -2a \\
\tau_3 &= 0
\end{align}
$$
Note that $\Delta_i$ only depend on $a$! When $a < 0$, then we a saddle one at $\mathbf{p}_1^*$ while $\mathbf{p}_2^*$, $\mathbf{p}_3^*$ are linear centres only -- that is, they are non-hyperbolic (the eigenvalues of the Jacobian are pure imaginary), and we cannot say much more about it without further analysis.
The situation is reversed when $a < 0$, with $\mathbf{p}_1^*$ being a non-hyperbolic linear centre, and $\mathbf{p}_2^*, \mathbf{p}_3^*$ being saddles. The fact that things switch from being marginally stable to being linear centres should give us a clue that we might want to test for the existence of Hopf Bifurcations.
Let's see if there are any conserved quantities in the system that we can make use of in determining the actual stability of the linear centres. A quantity $E(x, y)$ is conserved if $\dot{E} = 0 = \nabla E \cdot \mathbf{f}$:
$$
\begin{align}
&\quad\; \frac{\partial E}{\partial x}y + \frac{\partial E}{\partial y}(-ax - bx^3) = 0 \\
&\Rightarrow \frac{\partial E}{\partial x} = (ax + bx^3) \wedge \frac{\partial E}{\partial y} = y
\end{align}
$$
So, you can do partial integration and stuff (I am getting lazy, and will update my post later properly) and we should find that:
$$E(x, y) = \frac{ax^2}{2} + \frac{bx^4}{4} + \frac{y^2}{2},$$
is a conserved quantity. This implies that trajectories of the phase point always lie on level sets of $E$. Using Wolfram Alpha with $a = -1$ and $b = 1$, we can see that there are clearly closed orbits around the minima of the conserved quantity (which correspond to the fixed points of $\mathbf{f}$):
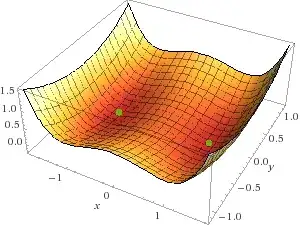
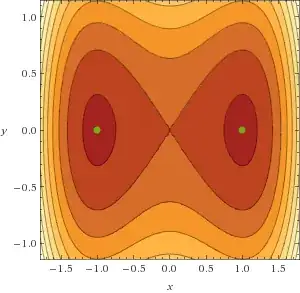
Now when $a = 1$ and $b = -1$ we see:

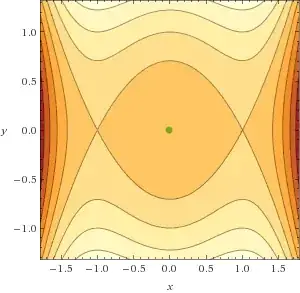
So the origin flipped from being a saddle point, to a centre with orbits around it (as you can see from the contour map!).
When $a = -1 < 0$ and $b = -1 < 0$ we see:
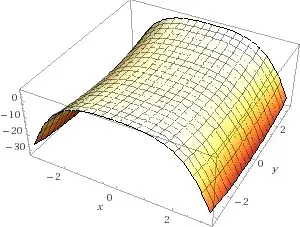
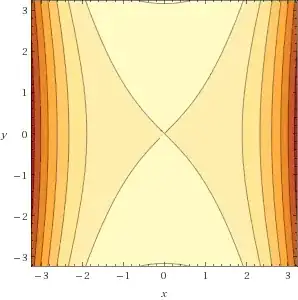
When $a = 1 > 0$ and $b = 1 > 0$ we see:
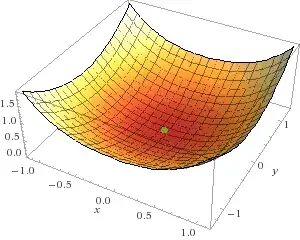
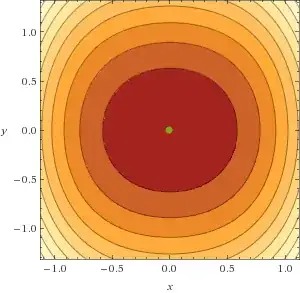
So, we go from having marginal stability to oscillations.
The comments bear witness to our confusion regarding whether these are simply degenerate Hopf bifurcations, or whether the pitchfork-like nature of the bifurcations has some signficance worth a name. Ultimately, I had to ask my instructor since I was unable to find a good answer on my own. I quote him here:
The equation is conservative, or Hamiltonian. There is a theory of
bifurcations for Hamiltonian systems, different from the "generic"
bifurcation theory because of the additional structure. What the
Duffing oscillator is experiencing is usually called a "Hamiltonian
pitchfork" bifurcation (fix $b$, vary $a$ through $0$). See p.399 of:
http://people.mbi.ohio-state.edu/golubitsky.4/reprintweb-0.5/output/papers/hamiltonian_87.pdf
for example.







