14

I was reading about one one functions and found out that they cannot have maxima or minima except at endpoints of domain. So their derivative , if it exists, must not change it sign , i.e. , the function should be either strictly increasing or strictly decreasing. From this I've a feeling that all continuous one one functions must be differentiable . Is this true?

A Googler
  • 3,443

4 Answers4

36

Not by a long shot. Take, for example, the function

$$f(x) = \begin{cases}x & x\leq 0\\ 2x & x\geq 0\end{cases}$$

Which is continuous and one-to-one on $\mathbb R$, but is not differentiable at $0$.

This is of course just one example, but in general, any time you "stick" two functions together at a point where their derivatives are not equal, like in my example, you can cause the resulting function to have a point at which it is not differentiable.

5xum
  • 126,227
  • 6
  • 135
  • 211
  • 4
    This one is good. But it doesn't "feel" good enough. I mean, your function is not differentiable on $\Bbb R$, but it's still differentiable almost everywhere. – Kitegi Apr 14 '15 at 08:54
  • Thank you! Do you think there can be a continuous one one function not differentiable at infinitely many points ? Or even nowhere differentiable? – A Googler Apr 14 '15 at 08:56
  • @AGoogler Yes. For the first, you can imagine a straight line drawn through the points $(0,0), (\frac12, \frac1{\sqrt2}), (\frac13, \frac1{\sqrt3}), \dots$ which form a bijective function from $[0,1)$ to $[0,1)$. – 5xum Apr 14 '15 at 08:59
  • 1
    @AGoogler: I think you can adapt the Bolzano construction: take an oblique line segment and move its middle point vertically, halfway to the high endpoint; repeat recursively and you get an increasing curve, nowhere differentiable. –  Apr 14 '15 at 09:03
  • @YvesDaoust Awesome ! Can you tell me where did you read about it? Because I cannot find anything related to it after searching on google. – A Googler Apr 14 '15 at 09:09
  • 6
    No, an increasing function is differentiable a.e. – zhw. Apr 14 '15 at 09:10
  • @AGoogler: Just googled "fonction continue sans dérivée". –  Apr 14 '15 at 09:11
  • This is a good answer. However, seeing as your function is differentiable everywhere except at one point, don't you think "not by a long shot" is a bit of an exaggeration? – bof Apr 14 '15 at 09:15
  • @bof The not by a long shot refers to the fact that we can very easily (and with little theoretical knowledge) construct a very simple function that provides a counterexample. – 5xum Apr 14 '15 at 09:25
  • 5
    To me, "not by a long shot" does not mean "the counterexample is simple and easy to find'; rather, it means "the assertion is very far from the truth". There is no need to tell the OP that his "feeling" was totally wrong, when in fact his intuition was mostly right, in that a strictly monotone continuous function is differentiable almost everywhere. And, regardless of how wrong someone's conjecture may be, there is no need to intruduce the refutation with "hell no!" or "of course not!". – bof Apr 14 '15 at 09:45
  • @zhw. What does a.e. mean? – A Googler Apr 14 '15 at 09:48
  • 8
    @bof It was in no way meant as an insult to the OP when I wrote "not by a long shot". It is just my way of saying "no, and look, here is a very simple counterexample". As far as "being close to the truth" is concerned, a statement is either true or false, there is no "close" to being true. We can, arbitrarily, define the closeness, but then I say "'close' to me means hard to find a counterexample", so this statement is "far" from true. – 5xum Apr 14 '15 at 09:49
  • 1
    @AGoogler "almost everywhere". This means that the set of all points for which the statement is not true has a measure of zero. – 5xum Apr 14 '15 at 09:52
  • @bof (as well as zhw. , 5xum , YvesDaoust ; the system doesn't allow notifying multiple users ) : So does that mean it can be not differentiable only at finite number of points ? Where does the constructions given earlier by YvesDaoust fail then? Is it because the curve doesn't "converge" i.e. recursing it infinitely doesn't make sense because it doesn't lead to a well defined curve? Thanks a lot by the way. – A Googler Apr 14 '15 at 10:03
  • 1
    @AGoogler: All I know is what I read in Wikipedia: a monotonic function on an interval is differentiable almost everywhere (and has at most a countable set of points of discontinuity). I don't know the proof (for differentiability a.e.); I learned it once, but that was in a previous century. I never did learn the construction of nowhere differentiable continuous functions. – bof Apr 14 '15 at 10:13
  • @bof Thanks for the link. – A Googler Apr 14 '15 at 10:15
  • 8
    @AGoogler: For an example of an injective (increasing) continuous function that is non-differentiable in an uncountable number of points (but still of measure zero) take the Cantor function and add the identity to it to make it injective. – Marc van Leeuwen Apr 14 '15 at 12:03
  • 1
    @j_random_hacker: You are wrong, measure zero does not imply countable (though the converse is true). In fact see my previous comment to see that "countable" is just wrong here. – Marc van Leeuwen Apr 14 '15 at 12:38
  • @MarcvanLeeuwen What does measure zero mean? I'm starting to get confused. If there can be uncountably infinite number of non differentiable points , why does it make sense to say that such function is "almost everywhere" differentiable? – A Googler Apr 14 '15 at 12:38
  • @AGoogler Because there exist subsets of $\mathbb R$ which contain uncountably many points and have a measure of zero. And It is possible for $f$ to be differentiable everywhere but on a set of measure zero. Measure theory is a huge and fairly complicated mathematica field.. http://en.wikipedia.org/wiki/Measure_%28mathematics%29 – 5xum Apr 14 '15 at 12:40
  • @AGoogler Measure theory is more refined than set theory. For set theory all nonempty intervals are equally large (because one can construct bijections), but measure theory gives them different length (measure) nonetheless. Not every set is measurable, but a countable union of disjoint sets will be measurable if the sum of their measures converges, with that sum as measure. The Cantor set is obtained from removing from a unit interval a countable union of intervals whose measures sum to$~1$; thereby measure$~0$ is left for the Cantor set. But that does not make it a countable set. – Marc van Leeuwen Apr 14 '15 at 12:54
  • @MarcvanLeeuwen: You're right. In fact I made 2 mistakes in my comment: claiming that uncountably large sets have nonzero measure, and thinking that the part of bof's comment that mentioned countability was talking about differentiability (it was talking about continuity). Down it comes. – j_random_hacker Apr 14 '15 at 13:24
16

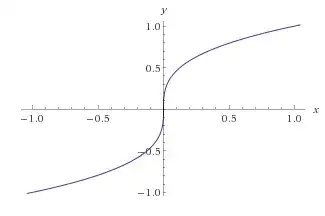
enter image description here

$x^{1/3}$ is not differentiable at $0$. See its graph above. It's qualitatively different from the example given by 5xum.

The Cantor function $ +\, x$ is an example of a function that's continuous and one-to-one, but non-differentiable at uncountably many points.

There's a limit to how bad an example can get. The set of points where a continuous one-to-one functions is non-differentiable always has Lebesgue measure $0$.

wlad
  • 8,355
  • I personally feel like this should be higher. Piecewise continuity is such a small generalization on continuity, while I feel like this is at the heart of the question. – A. Thomas Yerger Apr 15 '15 at 00:15
5

Well, you could do something like: Let $a_i$ be an enumeration of the rationals.

Define $f_i(x)$ as a continuous, nondecreasing function, strictly between $0$ and $1$ which is differentiable everywhere but $a_i$.

Define $g(x) := x + \sum_{i=0}^{\infty} f_i(x)\times 2^{-i}$

That should give a function that is continuous, but not differentiable at any rational number. (It's differentiable at every irrational number, though.)

Rusty
  • 2,958
ralphmerridew
  • 502
4

$\newcommand{\Reals}{\mathbf{R}}$There exists a strictly increasing continuous function $F:\Reals \to \Reals$ that fails to be differentiable at each rational number.

Let $(a_{k})_{k=1}^{\infty}$ be an enumeration of your favorite dense countable set $A$, such as the set of rational numbers, and $H:\Reals \to \Reals$ the unit step function $$ H(x) = \begin{cases} 0 & \text{if $x \leq 0$,} \\ 1 & \text{if $0 < x$.} \end{cases} $$ Form the sum of scaled translates $$ f(x) = \sum_{k=1}^{\infty} 2^{-k} H(x - a_{k}), $$ and its definite integral $$ F(x) = \int_{0}^{x} f(t)\, dt. $$

The following are easy "honors calculus"/elementary analysis exercises:

  1. The function $f$ is strictly positive (in fact, $0 < f(x) < 1$ for all real $x$), strictly increasing (hence Riemann integrable over an arbitrary compact interval), has a jump discontinuity at each point of $A$, and is continuous elsewhere.

  2. The function $F$ is continuous (as a definite integral), strictly increasing (positive integrand), strictly convex (increasing integrand), and differentiable at $x$ if and only if $f$ is continuous at $x$ (fundamental theorem of calculus, since $f$ has only jump discontinuities), hence non-differentiable at each point of $A$.

Community
  • 1
Andrew D. Hwang
  • 82,053