9

What is the smallest number $n$, that in any arrangement of $n$ points on the plane, there are three of them making an angle of at most $18^\circ$?

It is clear that $n>9$, since the vertices of a regular 9-gon is a counterexample. One can prove using pigeonhole principle that $n\le 11$. Take a edge of the convex hull of points. All the points lie to one side of this line. cut the half-plane into 10 slices of $18^\circ$ each. There can't be any points in the first and last slice. Thus, by pigeonhole principle some slice contains more than one point. So we have an angle of size at most $18^\circ$.

Now, for $n=10$, I can not come up with a counterexample nor a proof of correctness. Any ideas?

VividD
  • 16,196
Untitled
  • 351

2 Answers2

8

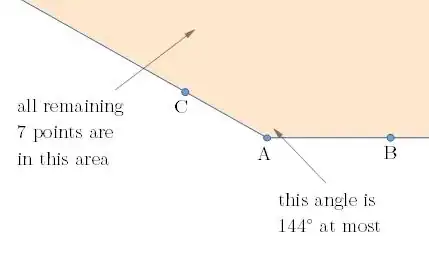
Hmm this appears pretty complicated. I hope there is a simpler solution.

Theorem. For any $n\ge3$ points on a 2D plane, we can always find 3 points $A,B,C$ such that $\angle ABC\le\frac{180°}n$. (OP's solution follows with $n=10$.)

Proof. Again we take an edge of the convex hull and all points lie on the other side of this edge. Let's say points $A$ and $B$ are on this edge.

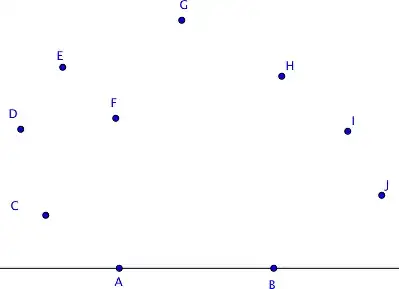
                      8 points C...J above line AB

Partition the half-plane into $n$ regions about point $A$. Name each region $A_1,\dotsc,A_n$, where a point $X$ inside $A_i$ means $\frac{180°}n(i-1)<\angle XAB\le \frac{180°}n\cdot i$.

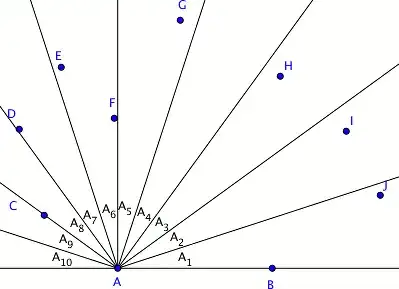
                      Partition half-plane into 10 regions

Do the same about point $B$. This will create $n$ other region $B_1,\dotsc,B_n$, where point $X$ in $B_j$ means $\frac{180°}n(j-1)<\angle XBA\le \frac{180°}n\cdot j$.

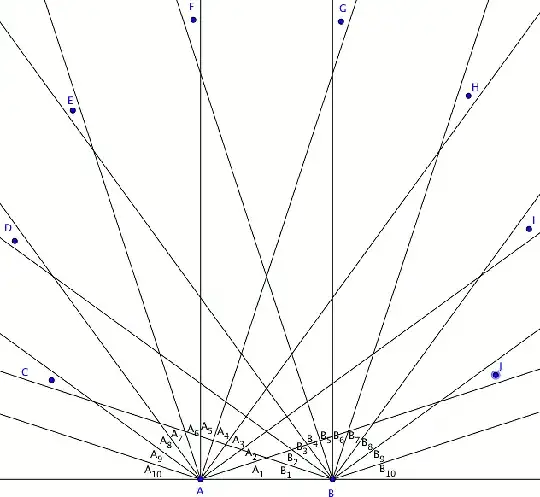
Welp, a total mess

If two points $X,Y$ can be found in the same region $A_i$, then we also have $\angle XAY \le \frac{180°}n$. That means only one point can exist in each of the region $A_i$ (there are $n-2$ points and $n-1$ valid regions). Same for $B_j$.

$A_i$ and $B_j$ may overlap, though only when $i+j< n+2$ (a):

\begin{array}{c|ccccccc} & A_2 & A_3 & A_4 & \cdots & A_{n-2} & A_{n-1} & A_n \\ \hline B_2 & ✓ & ✓ & ✓ & \cdots & ✓ & \color{red}{✓} & ✗ \\ B_3 & ✓ & ✓ & ✓ & \cdots & \color{red}{✓} & ✗ & ✗ \\ B_4 & ✓ & ✓ & ✓ & \cdots & ✗ & ✗ & ✗ \\ \vdots & \vdots & \vdots & \vdots & ⋰ & \vdots & \vdots & \vdots \\ B_{n-2} & ✓ & \color{red}{✓} & ✗ & \cdots & ✗ & ✗ & ✗ \\ B_{n-1} & \color{red}{✓} & ✗ & ✗ & \cdots & ✗ & ✗ & ✗ \\ B_n & ✗ & ✗ & ✗ & \cdots & ✗ & ✗ & ✗ \\ \end{array}

we immediately see that the points can only exist in the overlapping regions $A_i B_{n+1-i}$, to ensure no two point occupy the same column ($A_i$) or same row ($B_j$).

So for any $X$ in $A_i B_{n+1-i}$, we have:

\begin{align} \angle XAB &> \frac{180°}n(i-1) \\ \angle XBA &> \frac{180°}n(n-i) \\ \end{align}

For the triangle $\triangle ABX$, we need $\angle XAB + \angle XBA + \angle AXB = 180°$, thus

$$ \angle AXB < 180° - \frac{180°}n(i-1) - \frac{180°}n(n-i) = \frac{180°}n. $$

Note:

(a) if point $X$ exists in both $A_i$ and $B_j$ with $i+j\ge n+2$ then $$\angle XAB + \angle XBA > \frac{180°}n(i+j-2) \ge 180°,$$ which is impossible.

kennytm
  • 7,733
4

Suppose there are $10$ points. Let us construct the convex hull of these points. It has at most $10$ sides. This means it must have an angle that is at most $180° - 360°/10 = 144°$. Let us choose the vertex corresponding to such angle as point $A$, and its 2 neighboring points along the convex hull as points $B$ and $C$. In other words, we have situation pictured here:

enter image description here

Now, from $7$ points inside the angle $\angle CAB$ let us draw 7 lines to point $A$. This will divide the angle into 8 smaller angles, and one of them will be at most $144°/8 = 18°$.

Therefore, since there is a counterexample for $n=9$ (a regular 9-gon), the answer is

$$n=10$$

$$GENERALIZATION$$

The smallest number $n$, that in any arrangement of $n$ points on the plane, there are three of them making an angle of at most $180°/k$ is $$n=k$$.

The proof is virtually the same as for the case $k=10$.

VividD
  • 16,196