Proposition. Let $X$ be a closed subset of the sphere $\mathbb S^2$. Then $X$ is connected if and only if every connected component of $\mathbb S^2\setminus X$ is simply connected.
Necessary condition. Suppose some connected component $U$ of $\mathbb S^2\setminus X$ is not simply connected, that is, there exists a loop $\sigma:[0,1]\to U$ which is not contractible in $U$.
If $\sigma$ was an embedded $\mathbb S^1$ (a Jordan loop), then its complement in $\mathbb S^2$ would consists of two connected components $V,W$. Since $X$ is connected, only one could meet $X$, and the other would be contained in $U$, making $\sigma$ contractible in $U$. And this is the idea, although not that easy, because the loop, being just continuous may be very weird:
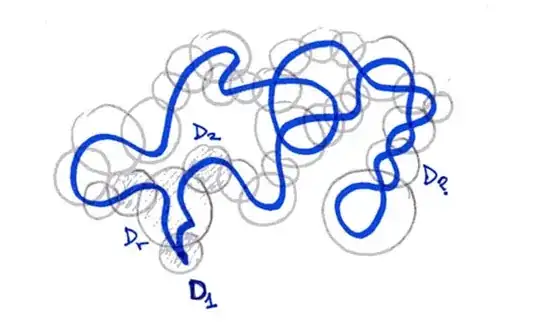
Denote $\varSigma$ the trace of $\sigma$ and pick a point $p\in\mathbb S^2\setminus\varSigma$ so that $\varSigma\subset U\setminus\{p\}\subset\mathbb S^2\setminus\{p\}\equiv\mathbb R^2$. The rough argument is to replace the loop by a polygonal joining suitable points of $\varSigma$, which we can do locally by interpolation in small discs $D_i$ covering $\varSigma$. But again, as the picture above tries to show, this may be elusive:
in the case depicted the disc $D_r$ must be repeated as $D_2$ and $D_2$ renamed as $D_3$, and things get worse with other discs.
To do this properly, cover $\varSigma$ with discs $D_i\subset U$. Their inverse images $\sigma^{-1}(D_i)$ form an open covering on $[0,1]$ and it has a Lebesgue number $\rho>0$ such that for any partition $0=t_0<t_1<\cdots<t_r=1$ with $\rho\!>\!1/r\ $ each image $\sigma([t_{k-1},t_k])$ lies in a disc $D_{i_k}\subset U$.
Next the segment $J_k\subset D_{i_k}$ joining $\sigma(t_{k-1})$ to $\sigma(t_k)$ is parametrized by the interval $[t_{k-1},t_k]$ to get a finite polygonal loop $\gamma:[0,1]\to \bigcup D_i\subset U$. This $\gamma$ is homotopic to $\sigma$ by $H_s=(1-s)\sigma+s\gamma$; notice here that linear interpolation remains inside the $D_{i_k}$'s. This guarantees $\gamma$ is not contractible in $U$, as $\sigma$ was not.
Now, $\gamma$ being a finite polygonal loop, it is indeed a finite union of polygonal Jordan loops, and some of them $L$ must be not contractible, hence we have in the end a polygonal Jordan loop $L\subset U$ and for this so simple loop the argument sketched at the beginning does work to get a contradiction.
Notice also that we are using the Jordan-Brouwer theorem, but the cheap case of a polygonal Jordan loop!
Sufficient condition. Suppose $X\subset\mathbb S^2$ is closed but not connected, say $X=Y\cup Z$ were $Y,Z$ are disjoint closed subsets of the sphere. We must construct a non-contractible loop $\sigma:[0,1]\to\mathbb S^2\setminus X$.
Here I will use some Differential Topology.
First we take a smooth function $f:\mathbb S^2\to\mathbb R$ which is $\equiv-1$ on $Y$ and $\equiv1$ on $Z$ (Uryshon's smooth function). Then we approximate $f$ by $g:\mathbb S^2\to\mathbb R$ which is $<0$ on $Y$ and $>0$ on $Z$ and is transversal to $\{0\}\subset\mathbb R$. Consequently, $C=g^{-1}(0)$ is a compact smooth curve, hence a finite union of smooth Jordan curves, say $C=C_1\cup\cdots\cup C_s$; by construction $C\cap X=\varnothing$. Each $C_\ell$ disconnects $\mathbb S^2$ (truly Jordan-Brouwer), hence $C_\ell$ has a regular smooth equation $g_\ell:\mathbb S^1\to\mathbb R$, which is a smooth function transversal to $\{0\}$ such that $C_\ell=\{g_\ell=0\}$. Of course $C_\ell$ has such local equations, but there is a problem with the choice of sign. Now as the curve disconnects one chooses the sign to be constant in a fixed component of the complement, and then the local equations can be glued well by means of a partition of unity. (This is too sketchy, but is the essential thing. Thinking of a non-disconnecting circle in a torus helps to see what's going on.)
An important fact is that any smooth function $h:\mathbb S^1\to\mathbb R$ vanishing on $C_\ell$ is a multiple of the equation $g_\ell$, that is, $h=h_\ell\cdot g_\ell$. Indeed, (i) locally at $C_\ell$ this reduces to the case $g_\ell=y$ in the plane, an easy Calculus exercise, and (ii) off $C_\ell$ one can divide by $g_\ell$ because it has no zero.
It follows that there is a factorization $g=ug_1\cdots g_s$, where $u$ is a smooth function nowhere zero. Thus $u$ has constant sign on $\mathbb S^2$, and since $g$ changes sign form $Y$ to $Z$, some factor $g_\ell$ must do the same. For instance, $g_1$ is $<0$ at some point $p\in Y$ and $>0$ at some point $q\in Z$. Consider the connected component $U$ of $\mathbb S^2\setminus X$ that contains $C_1$ and the inclusions
$$
C_1\subset U\subset\mathbb S^2\setminus\{p,q\}=M.
$$
If $C_1$ was contractible in $U$ it would be in $M$. But dropping $p$ gives the plane and there the Jordan loop $C_1$ with $q$ in its interior (as Jordan loop). Thus $M$ is a plane minus one point and $C_1$ a loop around that point, hence $C_1$ cannot be contractible in $M$. We are done.
