1

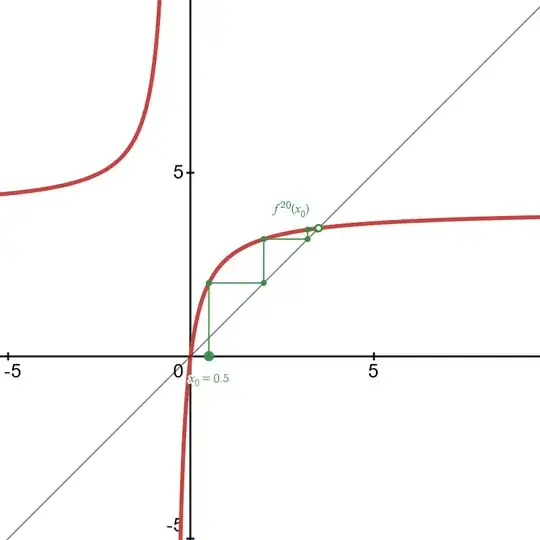
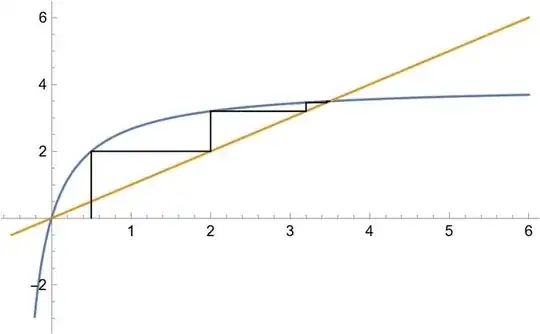
I am struggling making a cobweb diagram for the function

$$x_{t+1}=\dfrac{8x_t}{1+2x_t}.$$

So I understand when making the cobweb diagram, that I have to draw the line $y=x$. But where I have trouble understanding is how to draw the function in the graph. I am given the point $x_0 =0.5$ So I plug this into the function and get $2 = x_1$ and then I keep plugging in points. Do I graph points like $.5,2$ or $0,.5$?

Alp Uzman
  • 12,209
All About Groups
  • 596
  • I hope this doesn't come across as advertising. In the UK a lot of schools use a piece of software called Autograph. It draws cobweb diagrams for you... and shows Newton-Raphson working, too. – tomi Mar 13 '15 at 09:24

3 Answers3

2

Let the expression on the right be $g(x)$. The method converges (sometimes) to the solution of the equation $x=g(x)$.

The cobweb diagram illustrates the movement from first guess $x_0$ to second guess $x_1$ etc.

Draw a line from $(x_0,0)$ up to $(x_0,x1)$.

Then across to $(x_1,x_1)$.

Then up or down to $(x_1,x_2)$.

Then across to $(x_2,x_2)$.

Etc

tomi
  • 9,790
  • 1
  • 23
  • 39
0

Here is an interactive Desmos graph: https://www.desmos.com/calculator/bv6zwt0xnr

For the initial condition $x_0=0.5$ we get:

enter image description here

Alp Uzman
  • 12,209
0

Here is a Mathematica implementation, mostly so that I can refer to this post if I ever need to do a cobweb diagram in the future. I make no promises about it being the 'best' implementation. (As with the Desmos version, I'll take $x_0=0.5$.)

cobweb

x0 = 0.5;
f[x_] := 8 x/(1 + 2 x);
iterates = NestList[f, x0, 4];
Show[
 Plot[{f[x], x}, {x, -0.5, 6}],
 Graphics[Line[
   Prepend[
    Riffle[Transpose[{iterates, iterates}],
     Partition[iterates, 2, 1]], {x0, 0}]]]]
Semiclassical
  • 18,592