Evaluating $\frac{1}{2\pi j}\int_{c-j\infty}^{c+j\infty}x^{-s}\sigma ^{ms-m} [ \frac{\Gamma ( s )}{\Gamma ( s+2)}]^{m}ds$

Question

I have been trying to solve the problem for $m=3$: $$f(x)=\frac{1}{2\pi j}\int_{c-j\infty}^{c+j\infty}x^{-s}\sigma ^{ms-m}\left [ \frac{\Gamma \left ( s \right )}{\Gamma \left ( s+2 \right )} \right ]^{m}ds$$

Starting off, I have then simplified the problem to: $$f(x)=\frac{1}{2\sigma ^{m}\pi j}\int_{c-j\infty}^{c+j\infty}\left ( \frac{\sigma ^{m}}{x} \right )^{s}\frac{1}{s^{m}\left ( s+1 \right )^{m}}ds$$

For $m=3$ and finding the residues: $$\text{Res}\left ( \Gamma(s),0\right )=\frac{1}{2!}\lim_{s\rightarrow0}\frac{d^{2}}{ds^{2}}\left ( \frac{\sigma ^{3}}{x} \right )^{s}\frac{1}{\left (s+1 \right )^{3}}$$

$$\text{Res}\left ( \Gamma(s),-1\right )=\frac{1}{2!}\lim_{s\rightarrow-1}\frac{d^{2}}{ds^{2}}\left ( \frac{\sigma ^{3}}{x} \right )^{s}\frac{1}{s^{3}}$$

Using Cauchy's residue theorem, the simplified answer I obtain is: $$f(x)=\frac{1}{2\sigma ^{3}}\left [ 12\left \{ 1-\frac{x}{\sigma^{3}} \right \}-6log\left ( \frac{\sigma^{3}}{x} \right )\left \{ 1+\frac{x}{\sigma^{3}} \right \}+log\left ( \frac{\sigma^{3}}{x} \right )^{2}\left \{ 1-\frac{x}{\sigma^{3}} \right \} \right ]$$

To check the answer I obtained, I plot it out in MATLAB against the emperical solution and this is what I get (negative side of $x$ is mirror of positive side of $x$):

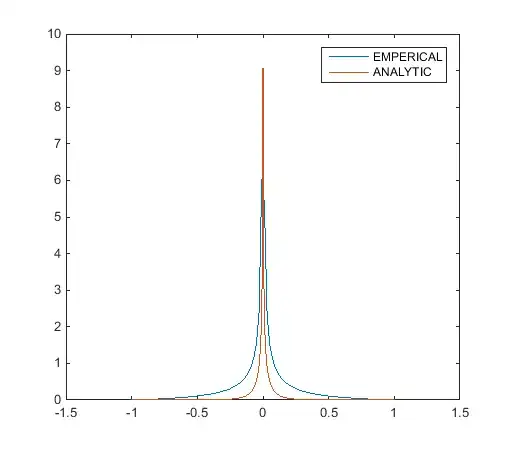
Where am I doing it wrongly? Is my final answer correct? Thanks

Answer:

There was nothing wrong with the analytical equation. And the problem is for $c>0$ and $x<\sigma$. Otherwise, $f(x)=0$. With that specified, the analytical expression obtained is correct!

*Thanks to @RonGordon

Answer 1

I do have something to add here. If the result is correct when $x \lt \sigma^3$, then the integral is zero when $x \gt \sigma^3$. The reason is convergence in the complex plane, similar to the problem I solved the other day. But the problem is incompletely specified, as I will demonstrate below.

Consider the integral

$$ \oint_C dz \frac{e^{t z}}{z^3 (z+1)^3} $$

where $t = \log{\left ( \frac{\sigma^3}{x} \right )}$ and $C$ is the standard Bromwich contour that consists of (1) the line $z=c+i y$, $y \in [-R,R]$ and (2) a circular arc of radius $R$ connected to the line at its endpoints, closed to the left of the line. Then the contour integral is equal to

$$\int_{c-i R}^{c+i R} ds \frac{e^{s t}}{s^3 (s+1)^3} + i R \int_{\pi/2-\delta}^{3 \pi/2+\delta} d\theta \, e^{i \theta} \frac{e^{R t \cos{\theta}} e^{i R t \sin{\theta}}}{R^3 e^{i 3 \theta} \left ( R e^{i \theta}+1\right )^3} $$

where $\delta \to 0$ as $R \to \infty$. In order that the residue theorem applies as $R \to \infty$, the integrals must converge. In this case, the second integral vanishes only when $t \gt 0$ To see this, note that the magnitude of the second integral is bounded by, as $R \to \infty$

$$\frac1{R^5} \int_{\pi/2}^{3 \pi/2} d\theta \, e^{R t \cos{\theta}} = \frac{2}{R^5} \int_0^{\pi/2} d\theta \, e^{-R t \sin{\theta}} $$

Note that convergence of this integral is achieved only when $t \gt 0$. In this case, the integral is bounded by (noting that $\sin{\theta} \le (2/\pi) \theta$)

$$\frac{2}{R^5} \int_0^{\pi/2} d\theta \, e^{-2 R t \theta/\pi} = \frac{\pi}{R^6} \left ( 1 - e^{-\pi R t} \right ) \le \frac{\pi}{R^6} \quad (R \to \infty)$$

What happens when $t \lt 0$? Obviously, the second integral above diverges as $R \to \infty$. In this case, we close to the right rather than the left. When we do that, that integral vanishes in the same manner as above.

Note that this is a very different situation than that when the integrand is $\Gamma(s)^2$, for example. There, I showed that the second integral vanishes when closed to the left, independent of the sign of $t$. That led to the integral representing the inverse of a bilateral Laplace, or Mellin, transform.

Back to this integral. When we apply the residue theorem, we find that we have, by definition of the constant $c$, situated the line to the right of all poles (i.e., $c \gt 0$). This is a consequence of defining the integral above as an inverse of a one-sided Laplace transform that demands causality, i.e., the inverse be zero when $t \lt 0$.

However, I am going to throw another wrench into the works. What if we set $c \in (-1,0)$? Well, the integral no longer represents an inverse Laplace transform, but so what? You never specified that it is: you never stated so, nor did you define $c$. In that case, the integral takes on a very different value:

$$\operatorname*{Res}_{z=-1} \frac{e^{t z}}{z^3 (z+1)^3} H(t) + \operatorname*{Res}_{z=0} \frac{e^{t z}}{z^3 (z+1)^3} H(-t)$$

where $H(t) = 1$ when $t \gt 0$ and $0$ when $t \lt 0$. I'll let you work out the details, but you need to specify this in your problem statement.