6

Obviously, for any polygon we can define at least $3$ different centroids:
$C1:\;$ mass center of the lamina;
$C2:\;$ mass center of vertices with equal masses;
$C3:\;$ mass center of the perimeter.

For the triangle $C1 = C2 \ne C3$; for common, even convex, polygon $C1\ne C2\ne C3$:

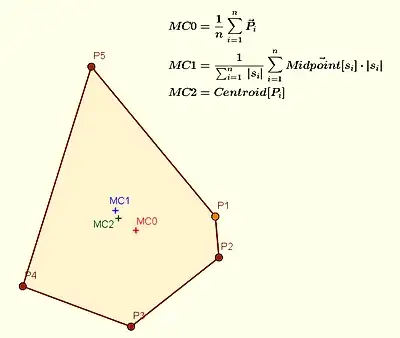
enter image description here

I'm interested: are there any theorems, facts or conjectures about these points?

Viera Čerňanová
  • 8,719
lesobrod
  • 877
  • Thanks for the pointer to the related question, Polygons with coincident area and perimeter centroids. – Joseph O'Rourke Mar 03 '15 at 18:58
  • Note that C1,C2,C3 are the centroids of the 2-skeleton, 0-skeleton, 1-skeleton respectively-- perhaps they would be better named C0,C1,C2. The only interesting fact I can think of is that for a simplex, the centroids of the 0- and n-skeleton are equal... not sure why. Also see somewhat related question http://math.stackexchange.com/questions/1780630/can-a-convex-polygon-have-only-one-boundary-point-at-locally-maximum-distance-fr – Don Hatch May 12 '16 at 07:32

0 Answers0