Is this plus sign a covering space of $S^1 \vee S^1$?

Question

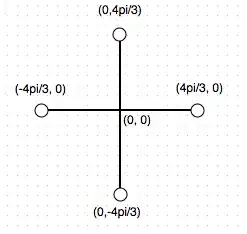
Consider this space, where open circles denote missing endpoints: space

Hatcher (p57) says that "every covering space of $S^1\vee S^1$ is a [2-oriented] graph." The above space is not a graph since the endpoints are missing.

But it looks to me like a covering space for $S^1\vee S^1$ under the projections $(x,0)\mapsto C_L(x)$ and $(0,y)\mapsto C_R(y)$, where $C_L(\theta)$ is the point at angle $\theta$ on the left circle. (We define the wedge point as $\theta=0$.)

Is it truly a covering space?

A simpler example that exhibits the same features: $[0, 2\pi) \to S^1$, $\theta \mapsto e^{i \theta}$ is not a covering space, can you see why? — Najib Idrissi, Feb 07 '15 at 10:26

score 5 · Accepted Answer · edited Apr 13 '17 at 12:20

It is not difficult to check that

if $p:X\to Y$ is a covering, $Y$ is compact and the fibers of $p$ are finite, then $X$ is compact.

Alternatively, you can use the fact that

if $p:X\to Y$ is a covering space and $Y$ is path-connected, all fibers of $p$ have the same cardinal.

You can also notice that your space is contractible, so that if it is a covering space, then it is the universal covering space (because it is simply connected) and the group of covering transformations would be the fundamental group of $S^1\vee S^1$. Now your space has no fix-point-free self-homeomorphism (the cross point is fixed by all self-homeos) so we would then conclude that $S^1\vee S^1$ is simply connected, and it isn't.

Is this plus sign a covering space of $S^1 \vee S^1$?

1 Answers1