Logistic family and chaos

Question

It is a well known fact that the map $f(x)=4x(1-x)$ is chaotic on $[0,1]$. By chaotic I mean the usual definition, i.e.:

a) the periodic points of $f$ are dense in $[0,1]$,

b) $f$ is topologically transitive,

c) $f$ exhibits sensitive dependence on initial conditions

One way to prove it is to show that the map: $$T(x)=\begin{cases} 2x, & \text{if }x\in[0,1/2) \\ 2-2x, & \text{if }x\in [1/2,1] \end{cases}$$ is chaotic, and then to show that there is a conjugacy between $f$ and $T$, which implies that $f$ is chaotic. According to Wikipedia for most values of $r>3.56995$ the function $f_r(x)=rx(1-x)$ is chaotic on a subset of $[0,1]$.

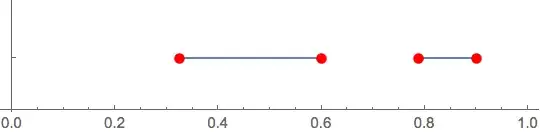
I am interested in proving that $f_{3.6}(x)=3.6x(1-x)$ is chaotic. By looking at the cobweb plot it seems that $f_{3.6}$ is chaotic on the interval $[0.324,0.9]$. I have tried to use a similar approach to the one described above to show that $f_{3.6}$ is chaotic, but I have not been able to find a conjugacy between $f_{3.6}$ and $T$. Does anybody know a way to show that $f_{3.6}$ is chaotic on $[0.324,0.9]$?

Answer 1

This map is certainly not chaotic on any invariant interval. It's likely that $f^2$ is chaotic on an interval smaller than the one you mention, but I don't have a proof.

As is well known, the critical orbit (the orbit of the critical point $1/2$, in this case) dominates the dynamics. The most famous fact along these lines is that an attractive orbit must attract a critical point. Even when the map is chaotic, the critical orbit is extra important through the kneading theory. So let's start by iterating the function from the critical point $1/2$ and examine the output. If I plot the first $2000$ iterates as points along the number line, I see something like so:

Thus, the orbit appears to be dense in the union of two sub-intervals. We can see what's going on by plotting $f^2$.

Note that there are two, invariant sub-intervals for $f^2$ with endpoints labeled in red in that figure. These are exactly the the first four iterates of $f$. $$(d,a,c,b) = (f(1/2), f^2(1/2), f^3(1/2), f^4(1/2).$$ On these sub-intervals, has nearly the classic unimodal look that gives rise to chaos. It's not quite there, though.

It should probably be pointed out that chaos on an entire interval is rare in the logistic family. This is made precise in the paper Generic Hyperbolicity in the Logistic Family. In fact, between any two $\mu$ values such that $f_{\mu}(x)=\mu x(1-x)$ has an attractive orbit, there is another such $\mu$ value. It follows that the set of all $\mu$ values without attractive orbits is nowhere dense; this precludes the possibility that these $\mu$ values have chaotic intervals. It is much more common that the chaotic set is a Cantor set, arises in my answer here.

Answer 2

OK it appears that my question was harder than I thought. Luckily, I have found a paper that answers a question close to mine: http://pyu1.apmaths.uwo.ca/~pyu/pub/preprints/SY_DCDIS_B2007.pdf

They show that for any $r\in [3 + (2/3)^{1/2},4]$, there exists a compact and perfect invariant set $D ⊂ [0,1]$ such that $f_r$ is chaotic on $D$ (chaotic in the sense described in my question). In particular, they use the concept of snap-back repeller. It is not possible to use this approach for the case $r=3.6$ but it's still a proof that the logistic map is chaotic for values different from $r=4$, which was my main interest. Apparently, the claim that for most values of $r>3.569946$ the logistic map is chaotic has only been verified numerically.