I have to solve the following problem using homothety but I don't see where it is.
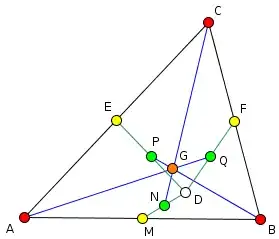
Given triangle $ABC$. $D$ is an arbitrary point inside the triangle. Points $M, E$ and $F$ are mid points of the sides $AB, AC$ and $BC$ respecitvely. Points $N, P$ and $Q$ are midpoints of $DM, DE$ and $DF$. Prove that the lines $AQ, BP$ and $CN$ intersect at a point.