Intuition behind the derivative of dirac delta function

Question

Let me first begin what I mean by saying the intuition behind the " $\delta'(x)$ ". For example the smooth approximations of the delta function looks like the following:

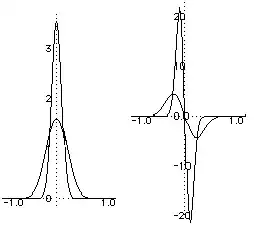
(Left:the smooth approximation of $\delta(x)$ Right:the smooth approximation of $\delta'(x)$)

And by using my intuition I can understand why $$ \int_{-\infty}^{\infty}f( \bar{x} )\delta(x-\bar{x}) \mathrm{d}\bar{x}=f(x) $$ because I can say that the delta function fires whenever $x=\bar{x}$ and picks up the value of $f(x)$ at that point and when I integrate over all values of x, I get my function f(x) back. In other words it is like building the function $f(x)$ from thin sticks, which has the same hight as the value of the function. (Although I know that this explanation is nowhere near mathematical, it helps me and others to understand -whatever that means- the concept easier.) When I learned about the derivative of the delta function and its following property I was utterly shocked: $$ \int_{-\infty}^{\infty}f(\bar{x})\delta'(x-\bar{x}) \mathrm{d}\bar{x}=f'(x) $$

Because no matter how long I think about the subject I was unable to build a correct intuition about this distribution. My question is this: Can you explain me intuitively why the derivative of the delta function gives arise to a derivative?

PS: I know why this is true mathematically (integrating by parts and so on).

Answer 1

Suppose the spikes in the smooth approximation to $\delta'(x)$ are located at $x=-h$ and $x=h$.

When $\bar{x} \approx x+h$, the smooth approximation to $\delta'(x-\bar{x})$ will be large and positive, so the integral will roughly pick up "something large" times $f(x+h)$. Similary, for $\bar{x} \approx x-h$, the integral will pick up the same large factor times $f(x-h)$, but with the opposite sign. So if that large factor turns out to be of the magnitude $\frac{1}{2h}$, the integral will be roughly $$ \frac{f(x+h)-f(x-h)}{2h} = \frac{\bigl(f(x) + h \, f'(x) + O(h^2)\bigr) - \bigl(f(x) - h \, f'(x) + O(h^2)\bigr)}{2h} , $$ which tends to $f'(x)$ as $h \to 0$.

Answer 2

Use the nascent delta function based on the hat function: $$ \delta_h(x) = \begin{cases} 0 & |x|\geq h \\ x/h^2 + 1/h & -h \leq x \leq 0 \\ -x/h^2 + 1/h & 0 \leq x \leq h \end{cases}. $$

The derivative of this nascent delta function is $1/h^2$ on $[-h,0],$ $-1/h^2$ on $[0,h],$ and 0 everywhere else. So $$ \int_{-h}^{h} \delta_h'(x)f(x) ,dx = \int_{-h}^{0} \frac{f(x)}{h^2} ,dx + \int_{0}^{h} \frac{-f(x)}{h^2} ,dx =

• \frac{F(h) - 2F(0) + F(-h)}{h^2}

$$ where $F$ is the antiderivative of $f.$ The limit of the rightmost term as $h\rightarrow 0$ is the negative second derivative of $F$ at 0, that is $-f'(0).$

To understand the origin of the higher order derivatives of the Dirac delta function, you need to use the normal distribution based nascent delta function: $$ \delta_h(x) = \frac{1}{h\sqrt{\pi}} \exp(-x^2/h^2). $$

In a computer algebra system, compute $$ \int_{-\infty}^{\infty} \delta_h^{(n)}(x-a) x^k ,dx $$

for some integer $n\gt 1$ and some integer $k \geq n.$ The answer will be $$ (-1)^n k! / (k-n)! a^{k-n} + \text{terms containing positive powers of $h$} $$ that is, $(-1)^n$ times the $n$th derivative of $x^k$ evaluated at $a$ in the limit $h\rightarrow 0.$

Answer 3

So you might have heard about the discrete difference. It's basically the discrete counterpart for derivatives. Its definition is DF[x] = F[x]-F[x-1]. Now imagine a continuous function f. If you look closely, what the integral of f with delta function's derivative is doing is taking something very similar to a discrete difference for f that is discretized at a really really small step size.