Checking that a $3$-D diagram is commutative

Question

When proving certain results I need to use commutative diagrams, some of which quite complicated. My question is:

Do we need to check every small square all the time to make sure that they are all commutative?

As an example, if we have the following diagram. If in my proof I wrote "Consider the following commutative diagram":

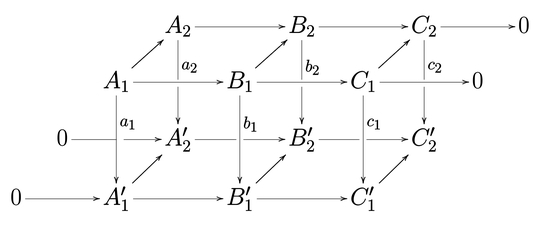
Before discussing anything else, I need to prove that it is indeed commutative. There are $11$ small squares to verify. When reading papers/books, I seldom see the author verifies every small square is commutative.

Is there any alternative other than checking all small squares, if I want to claim that a complicated diagram is commutative?

Answer 1

The most common way to get out of checking all the small squares is to have some monic or epic arrows in your diagram. For instance, suppose we knew the square from $B_1$ to $C_2$ was commutative, that $B_2\to C_2$ was monic, and that the large rectangle from $A_1$ to $C_2$ was commutative (that's a bit strong here since it's already epic, but this is discussion applies more generally.) Then by canceling the monic arrows we could deduce commutativity of the square from $A_1$ to $B_2$. Of course, you can dualize, and you can use this on cubes as well as rectangles: if you knew the top, bottom, front, back, and right faces of the $A,B$ cube were commutative then $A_2'\to B_2'$ being monic implies the left face is commutative.

But in general, even checking all but one square does not suffice, as you can see in your diagram: consider setting the $A_i'$ and $B_i'$ and all four $C$s to zero (then everything but the top left square automatically commutes, but we know nothing about the latter.)

Answer 2

If you are writing the proof, then you should at least explain how to check each one (maybe give a single example). If all the remaining are similar, then you can just say they are similar.

The really important thing is that you personally verified each fact. If you did not do it personally, how can you assert that you know it is commutative? If you can prove to yourself that it is true without checking each individual one, then you should be able to write the proof without checking each individual one.

Answer 3

Some relevant quotes, in which you might find cause for either comfort or despair:

Now these examples [of commutative diagrams] are only three of many more similar compatibilities that will come immediately to the reader's mind. I could make a big list, and in principle could prove each one on the list. However, I would be sure to need some more later, and already the list of ones I can think of offhand is too cumbersome to write down. And since the chore of inventing these diagrams and checking their commutativity is almost mechanical, the reader would not want to read them, nor I to write them. It would be comforting to know that such a list existed, or to have a meta-theorem saying that any such diagram one would dream up is commutative. However, both of these possibilities seem of an order of complexity to great to treat in these notes.


Unfortunately, I will have to use many of these compatitibilities in an essential way in what is to follow. Perhaps for each theorem in the sequel one could make a list of exactly which compatibilities are needed, and verity them, but even that is too clumsy at this stage. So I must ask the reader's indulgence. I believe in the truth of the theorems stated, and I hope to convince him of their truth also. But I have not verified every commutative diagram which is necessary for a rigorous proof, and I do not suppose that any reader will have the patience to do so either.

--Robin Hartshorne, Residues and Duality

The existing notes of SGA5 were both incomplete and unconvincing; I remember a talk by Illusie on the trace formula where he confessed to having been unable to prove compatibility of all the necessary diagrams. It is not enough to claim that the diagrams one writes "should" commute---especially when things as important (for me...) as Weil's or Ramanujan's conjectures depend on them!

---J.P. Serre, letter to Alexander Grothendieck

Answer 4

There is a relevant result called the Cube Lemma (see p. 43 of B. Mitchell, Category Theory, Academic Press, New York, 1965), which says that when all faces of a 3-dimensional cube commute, except possibly for the bottom face, and if the down-arrow into the source object of the bottom face is an epimorphism, then the bottom face must also commute. If all arrows are invertible morphisms, then the cube lemma says that if 5 of the 6 square faces commute, then the 6th also must commute. Under the same assumption of invertible morphisms (e.g., that the diagram is in a groupoid category), the result in Mitchell can be extended to hypercubes of all dimensions: if all the square faces in a particular (recursively-given) basis of the hypercube are commutative, then every face of the hypercube (not just the square faces) must be commutative. For the $n$-cube, $n \geq 20$, only about $4/n$ of the square faces are in the basis. See $\,$Cycle construction and geodesic cycles with application to the hypercube, ARS MATHEMATICA CONTEMPORANEA 9 (2015) 27–43, http://amc-journal.eu/index.php/amc/article/view/450/653. An example is given there (p. 41) of a diagram formed as the mod-2 sum of two commutative squares which is itself not commutative.

Answer 5

Normally the commutative diagram is a comprehensive collection of conditions. You can assume that each square is commutative and use that to make the conclusions.

But if the diagram is a theorem that you should prove, then you'll have to prove the commutativity of each square. But I have never seen that arrangement in exercises. However it could happen if all the homomorphisms where given.

But in the most cases the diagram is a condition from which you should make some few conclusions.