3

I'm trying to understand how one gets the long exact sequence in homology from a short exact sequence of chain complexes in an arbitrary abelian category.

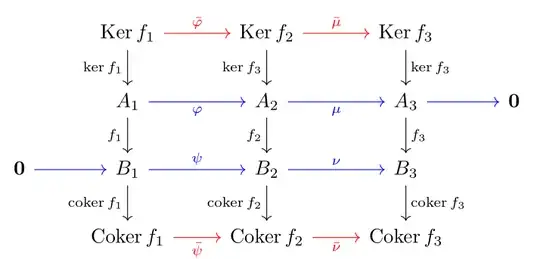
So far I have the commutative diagram below, with all rows exact: enter image description here

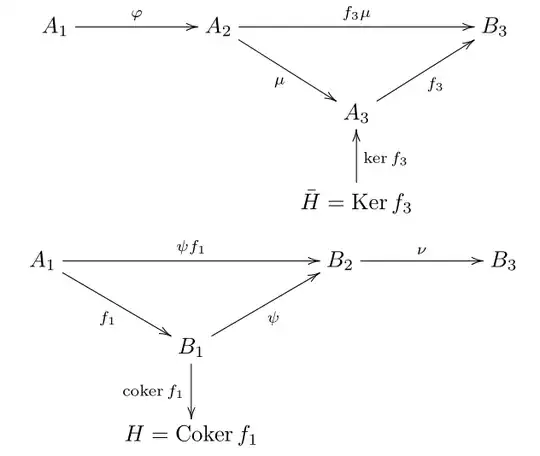
We examine the homologies enter image description here

Where $\bar H$ is the dual object of the homology, which is isomorphic to it.

Now the author of the book I'm following (Osborne's Basic Homological Algebra, p.231) says that the connecting morphism is defined as the homology map induced by $f_2$: $$(f_2)_\ast =\delta:\bar H\rightarrow H$$ I do not follow. How do we know such an arrow exists? In what precise sense is it induced by $f_2$?

Added: I would like a detailed explanation; "Just apply the universal properties" is not the answer I'm looking for.

Community
  • 1
  • 1
    Have you heard of the Snake Lemma? – Hayden Jan 19 '15 at 23:15
  • @Hayden yep. Unless I'm mistaken, I'm asking about the connecting morphism given by the snake lemma. My question comes from the process of proving it in the book I'm following, so I don't want to use it. –  Jan 19 '15 at 23:18
  • Ah, I see, just thought I'd mention it since you never explicitly said "snake lemma" (though your diagram is exactly what it applies to). – Hayden Jan 19 '15 at 23:19
  • I don't know a way to make $(f_2)*$ the image of $f_2$ under an operation $(-)*$, but an explicit (and element-free) definition of the connecting homomorphism is given here. – tcamps Jan 20 '15 at 03:49
  • @tcamps I don't understand "This then induces a map on quotients $B^{\prime \prime}/A \rightarrow A^\prime /\operatorname{Im}a$ which is precisely the desired map $\operatorname{Ker}c\rightarrow \operatorname{Coker}a.$" Explicitly, how is this map induced? I wasn't able to figure it out by myself. Also, it is $A^\prime /\operatorname{Im}a$ and not $A^\prime /\operatorname{Im}A$, right? –  Jan 20 '15 at 13:11
  • You can construct the connecting morphism by using the mapping cone. For instance, see Lemma 9.1.20 in my notes. – Zhen Lin Jan 21 '15 at 00:47
  • Exterior, you're absolutely right, that really isn't clear. @ZhenLin that will sometimes give the connecting homormophism in homology, but don't the 2-term chain complexes $A \to A'$ and $B \to B'$ have to cofibrant for $C \to C'$ to be quasiisomorphic to the mapping cone? Nice notes btw. – tcamps Jan 21 '15 at 23:22
  • There is no need to bring in any model structure. For some reason homological algebra is very nice. – Zhen Lin Jan 22 '15 at 01:08
  • @tcamps could you by any chance explain what's going on in detail? –  Jan 23 '15 at 08:50
  • @ZhenLin your notes look great, but I'd rather (at least for the first time) understand the "primitive proof". –  Jan 23 '15 at 08:50
  • 1
    Have you looked at this question and answer? – tracing Jan 27 '15 at 05:11
  • @tracing yes, that is the same answer tcamps mentioned in a previous comment, which I asked about above. –  Jan 27 '15 at 11:28
  • @Exterior: Sorry, I'd missed that. But I see you also had a question about the map $B''/A \to A'/\text{Im } A$. This is something general: we have a map $B'' \to A',$ and a sub object $A$ of $B''$. There is then an induced morphism from the quotient of $B''$ by $A$ to the quotient of $A'$ by the image of $A$ in $A'$. – tracing Jan 27 '15 at 12:31
  • @tracing I believe you, I just haven't been able to prove its existence. I would much appreciate a detailed walkthrough :) –  Jan 27 '15 at 12:57

0 Answers0