Dodecahedron has 20 vertices. I want to label them by $1,2,3,4,5$ with the following rule.
The five vertices of each face should have different labels.
Q. What is the number of ways of doing this? Is it unique up to some equivalence (for example- up to rotational symmetry of dodecahedron?)
This question can be answered without resorting to computer calculation. After labeling one face arbitrarily, and making one further arbitrary choice (for which there are two possibilities), the labeling is completely determined.
Summary: there are $240$ such labelings. If two labelings are considered equivalent when one is mapped to the other by one of the $60$ rotational symmetries of the dodecahedron, then there are four equivalence classes of labelings. It is a nontrivial fact that the $60$ rotations correspond to the even permutations of the five labels. Of the four equivalence classes of labelings, two are obtained from the other two by performing some odd permutation of the labels, say the swap $(45)$. Therefore there are two equivalence classes of labelings up to permutation of the labels. Finally, these two equivalence classes of labelings are mapped to each other by the reflection symmetry of the dodecahedron.
To expand on the issue of odd permutations: there are $5!=120$ permutations of the labels and hence $120$ ways to label a given face starting with a given vertex in, say, clockwise order. If two such labelings are considered equivalent when one is obtained from the other by rotating the labels around the face, then the equivalence classes are the circular permutations. Because $5$ is odd, the five elements of a circular permutation have the same parity. (Two elements of a circular permutation differ from each other by composition with a power of a five-cycle, which is an even permutation.) Therefore the parity of a circular permutation is well-defined.
In a subsequent paragraph I will describe the process of labeling all twelve faces. It turns out that the following properties hold.
There are $5!/5=24$ circular permutations and $24/2=12$ of each parity. Hence we can characterize a labeling by the parity of the circular permutations used; each circular permutation of that parity gets used exactly once in the labeling. Swapping two labels, say $4$ and $5$, changes the parity of every circular permutation in the labeling. If we insist that one face gets the circular permutation $12345$ then we fix the parity of the labelings of all faces to be even.
The labeling process goes as follows: pick a face and a starting vertex, and label the vertices of the face $12345$ in clockwise order. (The choice of $12345$ is arbitrary: any of the $5!=120$ permutations of $12345$ could be used.) At this point we have the labeling shown.
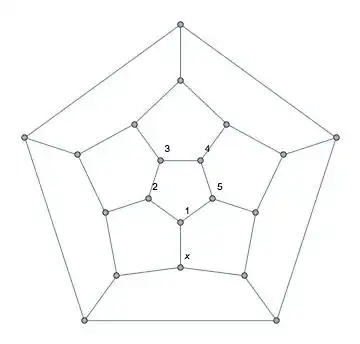
Unlabeled vertex $x$ adjacent to the vertex labeled $1$ cannot be labeled $1$, $2$, or $5$ since it is incident on faces on which those labels have already been used. Either $3$ or $4$ may be used. If we use $3$, then we have the following.
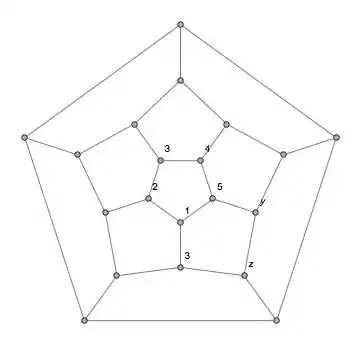
Unlabeled vertex $y$ adjacent to the vertex labeled $5$ can only be labeled $2$ since it is incident on faces on which $1$, $3$, $4$, and $5$ have already been used. Unlabeled vertex $z$ on the face that now has labels $3$, $1$, $5$, $2$ can only be labeled $4$. Proceeding counterclockwise, the labeling of the vertices all five faces surrounding the originally labeled face is completely determined in an analogous manner. The five vertices on the outer edges remain to be labeled, but their labels are fixed by similar considerations. The resulting labeling is shown below.
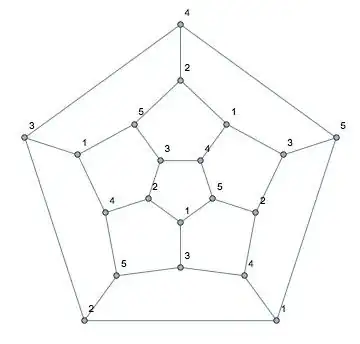
Returning to the initial state, if $x$ is labeled $4$ instead of $3$ we get the labeling below.
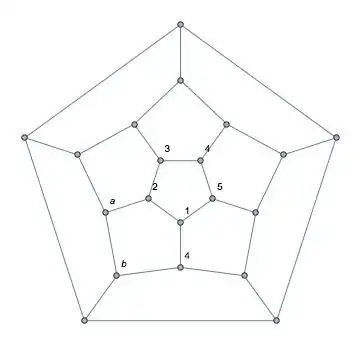
Vertex $a$ can only be labeled $5$ and vertex $b$ can only be labeled $3$. Proceeding clockwise this time, the labels of the vertices on the faces surrounding the originally labeled face are completely determined, as are the labels on the vertices on the outer edges. The resulting labeling is shown below.
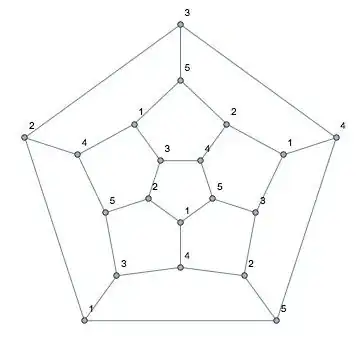
Given the labeling of the original face, these are the only two labelings possible. Since the same is true of any of the $120$ possible labelings of the original face, there are $240$ labelings in total. It may now be verified that in both of the labelings above the circular permutations on the $12$ faces are all different and all even.
That the faces are labeled by different circular permutations implies the neither of our labelings can be obtained from the other by rotating the solid: in one, the unique face labeled by the circular permutation $12345$ has $1$ adjacent to $3$, while in the other it has $1$ adjacent to $4$. It also implies that the $60$ labelings obtained by starting from one of the two labelings and rotating the dodecahedron are distinct. This accounts for $120$ of the $240$ labelings. We have already observed that the labelings obtained by rotation are the same labelings as are obtained by performing even permutations of the labels. This fact will be easily understood once we see what our two labelings really are. See below.
That the circular permutations in our two labelings are all even implies that we get $120$ further labelings by performing an odd permutation on the $120$ even labelings. This accounts for the remainder of the $240$ labelings.
In addition to the properties described above, we find that in both of our two labelings the circular permutations on antipodal faces are reverses of each other. For example, the face antipodal to the face labeled $12345$ is labeled $54321$. In our first labeling, $1$ is adjacent to $3$ in the face labeled $12345$, while $1$ is adjacent to $4$ in the face labeled $54321$. In our second labeling, the reverse is true. Since any reflection of the solid reverses the circular permutations on all faces, our two labelings are equivalent when reflection is taken into account.
So what are our labelings really? There is a geometrical answer to this question that makes it clear where all of the properties described above come from. Recall that a cube can be inscribed in the dodecahedron. The $12$ edges of the cube correspond to the $12$ faces of the dodecahedron. Of the set of $20$ vertices of the dodecahedron, a subset of size $8$ forms the vertices of a cube. In fact, there are five different cubes that can be inscribed in the dodecahedron in this way, each using a different subset of the $20$ vertices.
Each cube edge divides a pentagonal face into a triangle and a quadrilateral. Arrows may be placed on the cube edges by requiring that the arrow direction be compatible with a counterclockwise walk around the triangular segment of the face. There is then a bipartite division of the vertex set of the cube into a set of four source verticess (having three outgoing arrows) and four sink verticess (having three incoming arrows). Each vertex of a pentagonal face serves as a source vertex of exactly one of the five cubes and as a sink vertex of exactly one of the five cubes. If the five cubes are given labels, say $1$, $2$, $3$, $4$, $5$, then we get two labelings of dodecahedron vertices that have the property that every label is used exactly once on each dodecahedron face. In one labeling we assign each vertex the label of the cube of which it is a source vertex. In the other, we assign each vertex the label of the cube in which it is a sink vertex.
The two labelings we constructed above can be understood as arising in this way if we first rotate the second labeling by $4\pi/5$ in the clockwise direction.
Since the two labelings reflect the same underlying geometry, it makes sense to combine them by labeling each vertex of the dodecahedron by an ordered pair $(x,y)$ where $x$ is the label of the cube in which it is a source vertex and $y$ is the label of the cube in which it is a sink vertex. Observe that $x$ and $y$ must be distinct and that each of the $5\cdot4=20$ pairs of distinct labels appears exactly once. The diagram below shows this labeling and one of the five cubes (the one with label $1$).
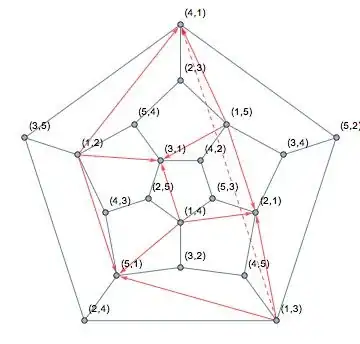
Since rotating the dodecahedron permutes the cubes, while maintaining the identification of sources and sinks, rotation amounts to a permutation of the cube labels. Reflection permutes the cubes, but also reverses the identification of sources and sinks, so it involves not permuting the cube labels, but also simultaneously swapping the elements of each pair.
Up to a $S_5$ permutation of the labels, there are exactly two possible labelings of the dodecahedron net:
1 - 2 - 3 - 4 - 5 - 1
| | | | | |
3 4 5 1 2 3
\ / \ / \ / \ / \ / \
5 1 2 3 4 5
| | | | | |
2 - 3 - 4 - 5 - 1 - 2
1 - 2 - 3 - 4 - 5 - 1
| | | | | |
4 5 1 2 3 4
\ / \ / \ / \ / \ / \
3 4 5 1 2 3
| | | | | |
1 - 2 - 3 - 4 - 5 - 1
Found through computer-aided systematic enumaration.
I upvoted the first answer but I would like to show how to solve this problem using Burnside. Before starting on that here are the first few solutions as found by a backtracking search.
1 - 2 - 3 - 4 - 5 - 1 | | | | | | 3 4 5 1 2 3 \ / \ / \ / \ / \ / \ 5 1 2 3 4 5 | | | | | | 2 - 3 - 4 - 5 - 1 - 2 * 1 - 2 - 3 - 4 - 5 - 1 | | | | | | 4 5 1 2 3 4 \ / \ / \ / \ / \ / \ 3 4 5 1 2 3 | | | | | | 1 - 2 - 3 - 4 - 5 - 1 * 1 - 2 - 3 - 5 - 4 - 1 | | | | | | 3 5 4 1 2 3 \ / \ / \ / \ / \ / \ 4 1 2 3 5 4 | | | | | | 2 - 3 - 5 - 4 - 1 - 2 1 - 2 - 3 - 5 - 4 - 1 | | | | | | 5 4 1 2 3 5 \ / \ / \ / \ / \ / \ 3 5 4 1 2 3 | | | | | | 1 - 2 - 3 - 5 - 4 - 1 1 - 2 - 4 - 3 - 5 - 1 | | | | | | 3 5 1 2 4 3 \ / \ / \ / \ / \ / \ 4 3 5 1 2 4 | | | | | | 1 - 2 - 4 - 3 - 5 - 1 1 - 2 - 4 - 3 - 5 - 1 | | | | | | 4 3 5 1 2 4 \ / \ / \ / \ / \ / \ 5 1 2 4 3 5 | | | | | | 2 - 4 - 3 - 5 - 1 - 2 1 - 2 - 4 - 5 - 3 - 1 | | | | | | 4 5 3 1 2 4 \ / \ / \ / \ / \ / \ 3 1 2 4 5 3 | | | | | | 2 - 4 - 5 - 3 - 1 - 2
These were computed with the a Perl program which produced the following count of admissible and of unique assignments:
$ ./dd.pl 1>/dev/null 240 2
thus confirming the result from the first responder.
This is the Perl code:
#! /usr/bin/perl -w
#
sub search {
my ($pos, $vals, $vseq,
$faces, $inc, $cref, $uref) = @_;
if($pos == 20){
printf "%d - %d - %d - %d - %d - %d\n",
@$vals{qw/W1 W2 W3 W4 W5 W1/};
printf "| | | | | |\n";
printf "%d %d %d %d %d %d\n",
@$vals{qw/X1 X2 X3 X4 X5 X1/};
printf " \\ / \\ / \\ / \\ / \\ / \\\n";
printf " %d %d %d %d %d %d\n",
@$vals{qw/Y1 Y2 Y3 Y4 Y5 Y1/};
printf " | | | | | |\n";
printf " %d - %d - %d - %d - %d - %d",
@$vals{qw/Z1 Z2 Z3 Z4 Z5 Z1/};
if(join('-', @$vals{qw/W1 W2 W3 W4 W5 W1/})
eq '1-2-3-4-5-1'){
printf " *";
$$uref++;
}
printf "\n\n";
$$cref++;
return;
}
my $what = $vseq->[$pos];
foreach my $nxt (1..5){
$vals->{$what} = $nxt;
my $admit = 1;
foreach my $f (@{ $inc->{$what} }){
my ($empty, %seen) = (0);
foreach my $v (@{ $faces->[$f] }){
if($vals->{$v} == -1){
$empty++;
}
else{
$seen{$vals->{$v}} = 1;
}
}
if(scalar(keys %seen) + $empty != 5){
$admit = undef;
last;
}
}
if(defined($admit)){
search($pos+1, $vals, $vseq,
$faces, $inc, $cref, $uref);
}
$vals->{$what} = -1;
}
}
MAIN: {
my $faces
= [[qw/W1 W2 W3 W4 W5/],
[qw/W1 W2 X1 X2 Y1/],
[qw/W2 W3 X2 X3 Y2/],
[qw/W3 W4 X3 X4 Y3/],
[qw/W4 W5 X4 X5 Y4/],
[qw/W5 W1 X5 X1 Y5/],
[qw/X2 Y1 Y2 Z1 Z2/],
[qw/X3 Y2 Y3 Z2 Z3/],
[qw/X4 Y3 Y4 Z3 Z4/],
[qw/X5 Y4 Y5 Z4 Z5/],
[qw/X1 Y5 Y1 Z5 Z1/],
[qw/Z1 Z2 Z3 Z4 Z5/]];
my $vseq =
[qw/W1 W2 W3 W4 W5/,
qw/X1 X2 X3 X4 X5/,
qw/Y1 Y2 Y3 Y4 Y5/,
qw/Z1 Z2 Z3 Z4 Z5/];
my $inc = {};
for(my $f = 0; $f < scalar(@$faces); $f++){
foreach my $v (@{ $faces->[$f] }){
push @{ $inc->{$v} }, $f;
}
}
my $vals= {};
foreach my $v (@$vseq){
$vals->{$v} = -1;
}
my ($count, $uniq) = (0, 0);
search(0, $vals, $vseq,
$faces, $inc, \$count, \$uniq);
print STDERR "$count $uniq\n";
}
Now to solve this using Burnside we need to compute the average of admissible assignments fixed by the $120$ elements of the full symmetry group of the dodecahedron, which includes not only rotations but also reflections. There is a classification of the rotations at this MSE link.
We start the count with the identity. It fixes all $240$ assignments from above. We will see that this is the only permutation that contributes. Next, rotations about an axis passing through the centers of opposite faces, contribution zero, because the unique five vertices of these faces are on the same cycle but cannot be fixed because they are distinct. Rotations about an axis passing through oppositee vertices create three-cycles of the vertices adjacent to the two vertices but adjacent ones of these are on the same face and hence different and not fixed by the rotation. Finally rotations about the centers of opposite edges fix those edges but the assignment on these is different,again for a zero contribution.
We will defer the study of the reflections to a later time.
The conclusion is that only the identity contributes to the Burnside count, giving a result of $$\frac{240}{120} = 2,$$ confirming the result from the Perl script.
Addendum Dec 31 2016. It would seem that the reflections leave just one orbit (must be one or two orbits, divisors of two).
