1

This is a problem from Discrete Mathematics and its Applications enter image description here

My question is on 9g. Here is my work so far 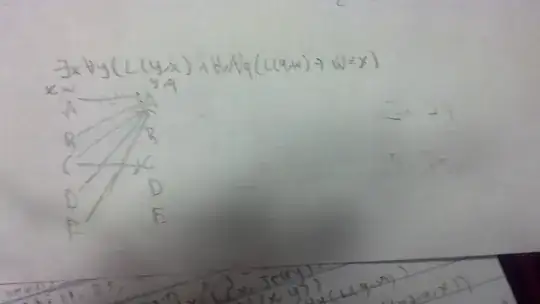enter image description here

I am struggling with the exactly one person part. The one person whom everybody loves is pretty straight forward ( ∃ x∀y(L(y,x)). I am trying to apply the method that Alan gave in How to express exact quantifier in this situation? from my other question. From what I have, if I know that x is a possibility(one, exists), I have to iterate over all the rest of the domain to ensure that there are no other possibilities(check against x) That's what I tried doing with the conjunction. However, this doesn't work because in my diagram, A is the exact one person whom everybody loves. I also showed that C loves C. Once q and w take up C and C (go through all the values in the domain) w, which is C, is not A, which means the whole expression is false because the implication is false but the expression shouldn't be false(A is the only one in the diagram whom everybody loves. C loving C should not have an effect) Is there any way else I can restructure the nested quantifier so i can still iterate through and see if there are any others that everybody loves?

Community
  • 1
committedandroider
  • 1,884

2 Answers2

0

Following the approach in the link, you would write $\forall y L(y,x) \wedge \forall z L(z,w) \implies w=x$

Ross Millikan
  • 383,099
  • you wouldn't need any quantifiers for x and w? – committedandroider Jan 14 '15 at 04:39
  • No. That is the point. It says that if $x$ is loved by everybody and $w$ is loved by everybody, they are the same. – Ross Millikan Jan 14 '15 at 04:49
  • Would this be equivalent? (∃x∀yL(y,x) ∧∃z∀wL(w,z)) -> w=z – committedandroider Jan 14 '15 at 04:52
  • No because all the variables before the implication are bound, so are dummies. The antecedent is a sentence, which is either true or false. It says nothing about $w$ or $z$. It would be the same as saying $(\exists a \forall b L(b,a) \wedge \exists c \forall d L(d,c))\implies w=z$ – Ross Millikan Jan 14 '15 at 04:58
  • without the ∃x, isn't x considered bounded as well, because it is bounded by the domain(all people in the world from the question). I don't get why not having that means the variable is no longer bounded – committedandroider Jan 14 '15 at 05:03
  • Bounded by the domain and bound in a sentence are completely different things. As you seem to be in computer science, bound in a sentence is like a local variable. It is not visible to anything outside the scope of the quantifier (function in CS), so we can change the name at will. – Ross Millikan Jan 14 '15 at 05:14
  • so that x you defined can take up anything, even say not a person, a dog perhaps? (original domain was all people in the world) – committedandroider Jan 14 '15 at 05:33
  • I suppose so, but then $L(y,x)$ should be false for $x$ not in the domain. I think all the variables are automatically limited to the domain. – Ross Millikan Jan 14 '15 at 05:38
  • Oh ok. so x and w should be bound to the domain - all people in the world. Does that mean x is the same person at all times(you don't include a quantifier, does that prevent x from changing?) – committedandroider Jan 14 '15 at 05:48
  • So when you don't use a quantifier, it acts like a free variable, take up any value? – committedandroider Jan 27 '15 at 06:08
  • That is correct. This is a sentence about $x$ and $w$, which says if they are both people that everybody loves, they are the same person. – Ross Millikan Jan 27 '15 at 15:01
  • oh in this case x is bounded by the domain and y is bounded by the sentence? You can't see y from outside its quantifier but you can see x outside y's bounded quantifier? – committedandroider Jan 27 '15 at 18:57
  • Yes you can see $x$ and $w$ outside the quanitifiers. I wouldn't call $y$'s quantifier bounded-it includes all the elements of the domain. A bounded quantifier in the naturals is something like $\forall y \lt N$, so it really only speaks about finitely many items. – Ross Millikan Jan 27 '15 at 20:19
0

The statement $\exists x \Big(P(x) \wedge \forall y \big(P(y)\to y=x\big)\Big)$ is the assertion of uniqueness.

"There exists a something for which the predicate is true and if the predicate is true for anything it must be that something."

So for "There is exactly one person whom everyone loves" we replace $P(\cdot)$ with $(\forall z\, L(z, \cdot))$

$$\exists x \Big((\forall z\, L(z,x))\wedge \forall y\big((\forall z\, L(z,y))\to y=x\big)\Big)$$

Note: this says "everyone loves a unique person". You may also interpret the statement as "everyone uniquely loves someone", which would be:

$$\forall w \exists x \Big(L(w,x)\wedge \forall y\big(L(w,y)\to y=x\big)\Big)$$

Equivalently:

The statement $\exists x \forall y \big(P(y)\leftrightarrow y=x\big)$ is another assertion of uniqueness.

"There exists a something such that if the predicate is true for anything it must be that something."

So for "There is exactly one person whom everyone loves" we replace $P(\cdot)$ with $(\forall z\, L(z, \cdot))$

$$\exists x \forall y\big((\forall z\, L(z,y))\leftrightarrow y=x\big)$$

Note: this says "everyone loves a unique person". You may also interpret the statement as "everyone uniquely loves someone", which would be:

$$\forall w \exists x \forall y\big(L(w,y)\leftrightarrow y=x\big)$$

Now can you do $(h)$ "there are exactly two people whom Lynn loves"?

Graham Kemp
  • 133,231
  • 1
    ∀zL(z,x) is saying everyone loves x. (∀zL(z,y)) is saying everyone loves y. I can't understand what the outside ∀y is saying in English though. For every person y, if everyone likes y, then y must the same x that we previously stated? – committedandroider Jan 14 '15 at 17:12
  • Yes. It means "There is an $x$ that everyone loves, and if there is any $y$ that everyone loves then $y$ is $x$." Thus the identity of $x$ is unique. – Graham Kemp Jan 14 '15 at 21:20