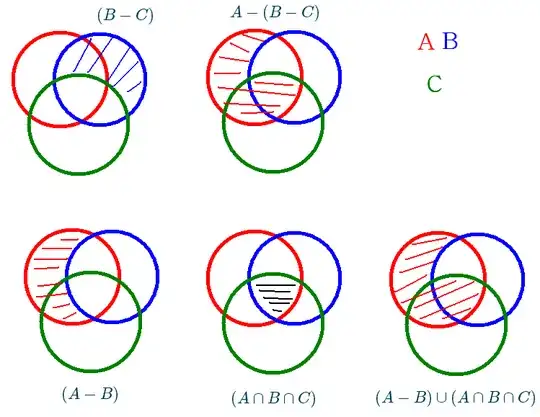
Prove $A-(B-C) = (A-B) \cup (A \cap B \cap C)$ :
What I think of doing is showing the LHS is a subset of the RHS and the RHS is a subset of the LHS, then the RHS = LHS.
$\Rightarrow$
We have $x \in A$, but $x \notin (B-C)$, thus $x \in (A-B)$ and then we see that $x \in (A-B) \cup (A \cap B \cap C)$. And we have the LHS a subset of the RHS.
$\Leftarrow$
3 cases:
1.) $x \in (A-B)$ only
from this we see that the RHS is a subset of the LHS
2.) $x \in (A \cap B \cap C)$ only
This is not possible. Exclude this from our discussion.
3.) $x \in (A-B) \wedge x \in (A \cap B \cap C) $
This is not possible. Exclude this from our discussion.
Thus, the RHS is a subset of the LHS, shown by case 1.
Since the LHS is a subset of the RHS and the RHS is a subset of the LHS, then the LHS = RHS and
$A-(B-C) = (A-B) \cup (A \cap B \cap C) $
Is this methodology right. I have more details in the proof I constructed but wanted to know if this method of thinking is good for the proof. Thanks!