When do 3 particles on the vertices of an Equilateral triangle meet?

Question

I am having a problem solving the following question. It says that

"3 particles A,B and C are situated at the vertices of an equilateral triangle ABC of side d at t=0. Each particle moves with a constant speed v. A always has its velocity along AB, B along BC and C along CA. At what time will the particles meet ? "

1. I fail to firstly understand why as my book says that they will meet at the centroid. If each particle has same speed and velocity is along te sides then they should never meet??

2. The next part of the solution says that velocity of A along AB and B along BC. so its component along BA is vcos60.

thus the separation decreases at the rate 3v/2.

how does the separation decrease rate. i cannot understand this practically.

last part is that since the rate is constant, time taken in reducing AB from d to 0 is 2d/3v that is the Answer which i have understood.

I basically dont understand how the separation is linked to the rate and this problem practically.

pls help...

Answer 1

Another way to look at how the separation decreases with time would be as follows.

Assumptions:

1. The initial length of the triangle is $a$.
2. All particles move with constant speed $v$.

Let at a certain instant of time $t$, the side length of the triangle is $x(t)$.

The image represents the position of the three particles at any instant of time $t$ and its subsequent position after a time $\Delta t$.

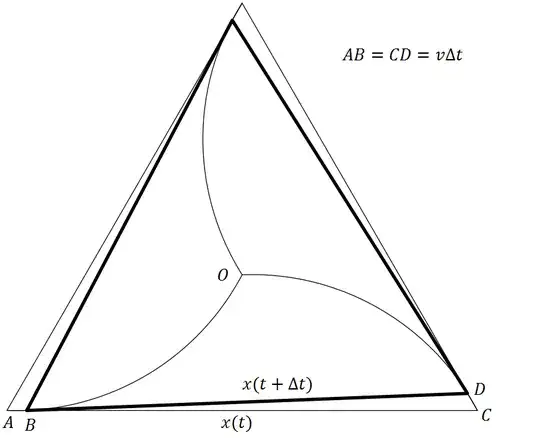
Do note that the angle $\angle BCD$ is always $60^0$.

Applying the cosine rule to the $\Delta BCD$, we have $$ \cos \frac{\pi}{3}=\frac{1}{2}=\frac{[x(t)-v\Delta t]^2 + [v\Delta t]^2 -[x(t+\Delta t)]^2}{2[x(t)-v\Delta t][v\Delta t]}$$

$$ \implies [x(t)-v\Delta t][v\Delta t]= [x(t)]^2 + 2[v\Delta t]^2 -2vx(t)\Delta t -[x(t+\Delta t)]^2 $$

$$\implies vx(t)\Delta t -[v\Delta t]^2 = [x(t)]^2 + 2[v\Delta t]^2 -2vx(t)\Delta t -[x(t+\Delta t)]^2$$

$$\implies [x(t+\Delta t)]^2 -[x(t)]^2=3[v\Delta t]^2 -3vx(t)\Delta t $$

Let $\big [x(t)]^2=A(t)$. The above equation becomes

$$\implies A(t+\Delta t) -A(t) = 3[v\Delta t]^2 -3v\sqrt{A(t)}\Delta t $$

$$\implies \frac{A(t+\Delta t) -A(t)}{\Delta t} = 3v^2 \Delta t - 3v\sqrt{A(t)}$$

Taking the limit $\Delta t \rightarrow 0$, the LHS becomes a derivative, and the first term of the RHS becomes zero.

$$\implies\frac{dA(t)}{dt}=-3v\sqrt{A(t)} $$

$$ \implies \frac{dA(t)}{\sqrt{A(t)}}=-3vdt$$

The above equation needs to be integrated within suitable limits to evaluate the change in length of the triangle with time.

At time $t=0$, length of side of triangle is $a$. At time $t$, the length of the side of the triangle is $x(t)$. The limits of integration in the LHS is from $a^2$ to $[x(t)]^2$.

$$\large \implies \int_{a^2}^{[x(t)]^2}\frac{dA(t)}{\sqrt{A(t)}}=\int_{0}^{t}-3vdt$$

$$\large \implies 2[|x(t)|-a]=-3vt$$

This equation describes the change in length of the side of the triangle with time.

To find out when the three particles will meet, we put $x(t=t_0)=0$ where $t=t_0$ is the time at which the three particles meet.

And thus, $\large t_0= \frac{2a}{3v}$

Answer 2

Phoenix87 has already answered it. More verbosely, you have: Particle A is hunting particle B, but B is moving. At each moment, the A will readjust its direction in order to keep facing B.

The direction of the B is also changing, because it is hunting particle C. And particle C is hunting particle A.

By symmetry, they will meet at the centroid.

If you see this, instead of fixed directions, you can already find the rate of approach. Consider a small interval of time, during each the directions may be considered unchanged. During this small amount of time, particle A is moving along the line AB at velocity V. Altough B is not moving exactly in the direction of A, its velocity has a component at the direction of A, which is vcos60. Therefore, A is approaching B at a rate equal to (v+vcos60).

Although the direction of each particle is changing, it's speed is constantly v and the particles keep the same position one to the other.

So the rate of approach is constantly (v+vcos60).

Since, the initial separation is d, you get t = d/(v+vcos60).

Answer 3

Slight variation of Tamojit's Method, after getting the equation:

$$ l^2 (t+ \delta t)= v^2 \delta t^2 + l^2 (t)+ v^2 \delta t^2 - 2lv \delta t - v \delta t (l - v \delta t)$$ Group and rearrange:

$$\frac{l^2 (t+ \delta t)- l^2 (t)}{\delta t} =3v^2 \delta t-3l v $$

Note that $l(t + \delta t) \approx l(t)$ and using $a^2 -b^2 = (a+b)(a-b)$ on LHS , we get:

$$ \frac{l(t+ \delta t) - l(t) }{\delta t} (2l) =3 v^2 \delta t - 3lv$$

Under the limit as $\delta t \to 0$, we arrive as:

$$ \frac{dl}{dt} = \frac{-3lv}{2}$$

The DE has solution:

$$ l(t) = - \frac{3}{2} v t + l(t=0)$$

Setting $l(t)=0$, and isolating for $t$, we find the required.

Answer 4

i think since the particles have identical motions and are at exactly equal diatances from each other their nature of motions are going to be exactly similar,that being the case they must meet at a point which shall be at equal distances from their starting points . this is possible only when the meeting point is a centroid by geometry

Answer 5

The velocities have a component perpendicular to the side also. So, from the problem delete the part "A always has its velocity along AB, B along BC and C along CA".