4

Solve:

$$z^6 + 1 = 0$$

That lie in the top region of the plane.

We know that:

$$(z^2 + 1)(z^4 - z^2 + 1) = 0$$

$$z = -i, i$$

We need to solve:

$$((z^2)^2 - (z)^2 + 1) = 0$$

$$z = \frac{1 \pm \sqrt{-3}}{2}$$

But this is incorrect. How to do this then?

Amad27
  • 11,551
  • 7
    It's incorrect because in the last step, you forgot to write $z^2$. – Raskolnikov Dec 22 '14 at 11:28
  • 1
    There are already good answers to the question, but if you're interested in a general formula for equations of the form $z^n = a$ like yours $z^6=-1$, then it is here in another similar question I answered. – Eff Dec 22 '14 at 16:41

4 Answers4

6

Only your last line is incorrect. What you should write is

$$z^2 = \frac{1\pm\sqrt{-3}}{2}$$

5xum
  • 126,227
  • 6
  • 135
  • 211
6

$$z^6=-1=e^{(2n+1)\pi i}$$ where $n$ is any integer

$$\implies z=e^{\dfrac{(2n+1)\pi i}6}=\cos\dfrac{(2n+1)\pi}6+i\sin\dfrac{(2n+1)\pi}6$$ where $0\le n\le 5$

Top region of the plane, $\implies$ the ordinate has to be $>0$

$\implies\sin\dfrac{(2n+1)\pi}6>0\implies0<\dfrac{(2n+1)\pi}6<\pi\iff0<2n+1<6\implies-.5< n<2.5$

$\implies n=0,1,2$

lab bhattacharjee
  • 279,016
  • 4
    This answer seems to miss the point of the question. – quid Dec 22 '14 at 14:29
  • @quid, This pattern, will not allow the fuss due to solving in algebraic way – lab bhattacharjee Dec 22 '14 at 16:09
  • The point of the problem OP means to solve seems to be just dealing with this "fuss." In addition, what do you do if you want to know the algebraic form of the soltions, now? Say, you want to know the real part of the solutions? Obviously you might reply that one knows the values of the triginometric functions there, but then one also knows the twelvth roots of unity at which point we might just say the problem is trivial. – quid Dec 22 '14 at 16:15
2

The simplest way of solving this equation is the method based on DeMoivre's Formula that Lab Bhattacharjee outlined.

That said, you can make your method work. You found the roots $z \pm i$ by setting the factor $z^2 + 1$ equal to zero. As Rasolnikov and 5xum noted, you should have obtained

$$z^2 = \frac{1 \pm \sqrt{-3}}{2}$$

when you set the factor $z^4 - z^2 + 1$ equal to zero.

Let $z = a + bi$, with $a, b \in \mathbb{R}$. Then

\begin{align*} z^2 & = \frac{1 \pm i\sqrt{3}}{2}\\ (a + bi)^2 & = \frac{1 \pm i\sqrt{3}}{2}\\ a^2 + 2abi - b^2 & = \frac{1 \pm i\sqrt{3}}{2} \end{align*}

Equating real and imaginary parts yields \begin{align*} a^2 - b^2 & = \frac{1}{2}\tag{1}\\ 2ab & = \pm\frac{\sqrt{3}}{2}\tag{2} \end{align*} Solving equation 2 for $b$ yields $$b = \frac{\pm\sqrt{3}}{4a}\tag{3}$$ Substituting this expression in equation 1 yields \begin{align*} a^2 - \frac{3}{16a^2} & = \frac{1}{2}\\ 16a^4 - 3 & = 8a^2\\ 16a^4 - 8a^2 & = 3\\ 16a^4 - 8a^2 + 1 & = 4 && \text{complete the square}\\ (4a^2 - 1)^2 & = 4\\ 4a^2 - 1 & = \pm 2\\ 4a^2 & = 3 && \text{since $a \in \mathbb{R}$}\\ a^2 & = \frac{3}{4}\\ a & = \pm \frac{\sqrt{3}}{2} \end{align*} Substituting this expression into equation 3 yields the four roots $$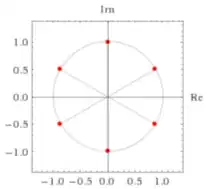z = \pm\frac{\sqrt{3}}{2} \pm \frac{1}{2}i$$ of the equation $z^4 - z^2 + 1 = 0$. As you can check, these roots correspond to the values $n = 0, 2, 3, 5$ in the formula Lab provided.

N. F. Taussig
  • 79,074
  • "The simplest way"...then let us start from scratch and see who has finished first with an explanation. Obvioulsy if you are willing to assume all kinds of things the problem is "simple." Upvoted though for giving the details to the question actually asked. – quid Dec 22 '14 at 15:41
0

In order to solve $\sqrt[2n]{-1}$:

  • Draw the unit circle
  • Draw the first solution, which is obviously $0+1i=\cos(\frac{\pi}{2})+\sin(\frac{\pi}{2})i$
  • Repeat $2n-1$ times: find the next solution by rotating the previous solution $\frac{\pi}{n}$ radians

For example, $\sqrt[6]{-1}$:

  • $\cos(\frac{ 3\pi}{6})+\sin(\frac{ 3\pi}{6})i$
  • $\cos(\frac{ 5\pi}{6})+\sin(\frac{ 5\pi}{6})i$
  • $\cos(\frac{ 7\pi}{6})+\sin(\frac{ 7\pi}{6})i$
  • $\cos(\frac{ 9\pi}{6})+\sin(\frac{ 9\pi}{6})i$
  • $\cos(\frac{11\pi}{6})+\sin(\frac{11\pi}{6})i$
  • $\cos(\frac{13\pi}{6})+\sin(\frac{13\pi}{6})i$

enter image description here

barak manos
  • 43,599