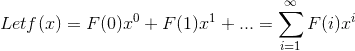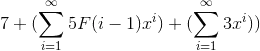0

I am having trouble understanding the process of expressing the following recurrence in its' closed form.

First of all, I do not really understand what "closed form" means. If someone could elaborate a little bit on this, it would be much appreciated.

Second, Could you explain the nature of the function itself, as in, what it is explicitly trying to do?

Here is the recurrence function:

$$F_{0} = 7$$

$$F_{N} = 5F_{N-1} + 3, \ \ ( N > 0 ).$$

Express $F_{N}$ in closed form

The final answer, should be the following:

$$\frac{31\cdot(5^N) - 3}{ 4}$$

Thank you so much for your help and additional explanations you may throw in. I am very lost in regards to what to do.

J.

UPDATE

Some of the process is here:

enter image description here

enter image description here enter image description here

Mauro ALLEGRANZA
  • 99,247
J Tarantino
  • 73
  • 5
  • "Closed form" is an analytical expression for the generic term of your sequence, that allows you to compute it without knowing the previous terms. In this case, $F(n)=31\cdot 5^n - 3/4$ is a closed form. – Giuseppe Negro Dec 09 '14 at 09:21
  • 1
    I would first take an ansatz $F_{N} = \lambda^{N}$ and then solve the homogeneous and particular parts separately. – Matthew Cassell Dec 09 '14 at 09:26
  • @GiuseppeNegro Do you know the process of how to get there? – J Tarantino Dec 09 '14 at 09:30
  • @Mattos: I’m unsure why did you change parentheses to subscript, but since original poster did not object, I rest it in place. – Incnis Mrsi Dec 09 '14 at 09:32
  • @Incnis Mrsi: Because sequences are usually defined by a subscript and also, the OP didn't use latex script at all so it was an educated guess as to what he was trying to ask. Now it looks even worse because we have $F_{N} = 5F(N-1)$. You'll need to edit it again now to have it as either $F_{N} = 5F_{N-1}$ or $F(N) = 5F(N-1)$ to avoid confusion. – Matthew Cassell Dec 09 '14 at 09:40
  • How do I fix it? I'm new to LaTEX :( – J Tarantino Dec 09 '14 at 09:47
  • Ok; first line, right hand side : fix index : $i$ must start from $0$. second line : RHS : fix exponent of $x$; it must be $i$. Third line : Ok. Add fourth line : $7+5x(sum(F(i-1)x^{i-1})$. – Mauro ALLEGRANZA Dec 09 '14 at 09:54
  • We can see also this post – Mauro ALLEGRANZA Dec 09 '14 at 10:21

1 Answers1

0

HINT

You have already the "final" exprssion :

$f(n) = (31 \times 5^n -3)/4$.

What you have to do is to prove - by induction - that it holds, i.e. that it satisfies the recurrence relation for $f(n)$.

(i) base case : $n=0$

For $n=0$ the recursive definition of $f(n)$ has : $f(0)=7$.

We have to check that it matches with the closed expression :

$$f(0) = (31 \times 5^0 -3)/4 = (31 -3)/4 = 28/4 = 7.$$

It's Ok.

(ii) induction step : assume that it holds for $n$ and show that it holds for $n+1$.

For the closed form, we can try with :

$f(n) = ac^n+b$.

For $n=0$ we have : $f(0)=7=a+b$; thus :

$a = 7-b$.

Using the recurrence relation : $f(n+1)=5f(n)+3$ we have : $ac^{n+1}+b=5(ac^n+b)+3$.

With $c=5$ we can compute $b = - \frac {3}{4}$ and so : $a = 7-b = 7 + \frac {3}{4} = \frac {31}{4}$.

Mauro ALLEGRANZA
  • 99,247