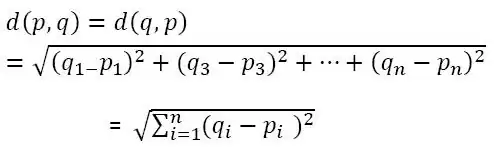As far as I can figure out, the author is attempting to show there is an algorithm which performs slightly better to the simple round robin scheduling algorithm by trying to find a time quantum which allows more of the processes in the queue to finish within a single trip, thereby reducing overall wait times. Too long of a time quantum makes it so that all processes finish their first trip essentially a first come first served algorithm, but that is undesirable as it may be unfair to simple or more important processes to be stuck behind a slow unimportant one. Too small of a time quantum makes it so that there is constant context switching, causing several processes to end at roughly the same time, causing long overall wait times.
As for the math he uses... I can't say that any of it seems right, or at least well explained. The author claims to "Calculate the Euclidean Distance of the cpu burst times of processes present in the ready queue" and defines:
Process ($P_i$): Number of processes in ready queue for $i = 1, 2, \dots, n$
Burst Time ($B_i$): Processing time required by each $P_i$
He proposes to set the time quantum to be used to be equal to $D \cdot Q_f$ where $D$ is the calculated "euclidean distance", and $Q_f$ is some experimentally found constant that he estimates to be around $0.4$. He goes on to compare the overall waiting times, turnaround times, and number of context switches for using a simple round robin quantum time and his proposed optimal round robin algorithm.
The author does not however explain what exactly he is taking the "euclidean distance of" and any and all attempts I have made at trying to figure that out have come up blank. There does not seem to be any logical explanation for how he comes up with his value for $D$. It is seemingly unrelated to mean, median, population standard deviation, sample standard deviation, third moments, distance to origin (assuming he treats all values as a combined point), total distance to origin (treating all as separate points), distance to a point (a, a+1, a+2, a+3, a+4), distance to a point (a,a,a,a,a), or others still. He also presents his value for $Q_f$ without any evidence or proof either. Honestly, it appears as though he pulled those numbers out of thin air to make the time waiting and turnaroundtimes come out nicer than the simple round robin algorithm.
He also gave no explanation for the values for the quantam times that the $SRR$ algorithm uses. According to other sources, a seemingly optimal time quantum could be calculated by the median of burst times for the processes in the ready queue, however that does not match what he uses.
Given the huge lack of detail, inconsistent formatting in certain places, apparent misuse or misunderstanding of euclidean distance, and typo in the distance formula itself, I would not trust this author or his work as it is presented and would seek other resources. If you would like a similar paper which seems better presented, this one appears to be well organized and explained: http://arxiv.org/ftp/arxiv/papers/1111/1111.5348.pdf
I will remind you however, that most of these papers present experimental results and attempt "proof by example" which is not proof at all. It is akin to saying "I believe every sunday is sunny because the past 10 sundays since I've started counting have all been sunny"
If you would like explanation on how to calculate euclidean distances between points, I suggest opening a new thread or reading other pages on the topic such as Calculate distance in 3D space
If you wish to understand what the author did to get his values, you will need to contact him directly.