Thin triangles vs Slim triangles in hyperbolic spaces

Question

What is the difference between thin triangles and slim triangles in $\delta$ hyperbolic spaces? Google search seems to consider thin and slim as synonyms and shows the same results for the two.

Answer 1

They are equivalent definitions of $\delta$-hyperbolicity with different but comparable values of $\delta$.

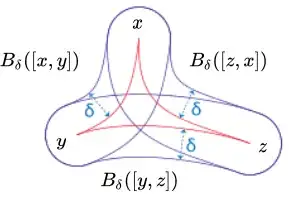
A geodesic triangle $\Delta(x,y,z)$ is $\delta$-slim if for any point $u$ on the side of geodesic segment $[x,y]$ the distance from $u$ to $[x,z] \cup [z,y]$ is at most $\delta$.

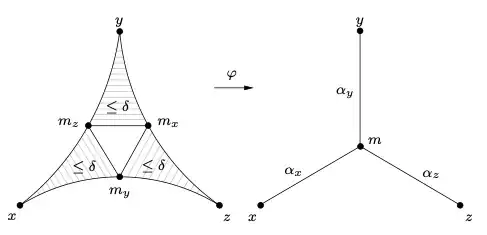
Let $m_x$ be the point of the geodesic segment $[y,z]$ located at distance $\alpha_y = (x|z)_y$ from $y$, where $(x|z)_y$ is the Gromov product of $x,z$ with respect to $y$. Then, $m_x$ is located at distance $\alpha_z = (x|y)_z$ from $z$ because $\alpha_y + \alpha_z = d(y,z)$. Analogously, define the points $m_y \in [x,z]$ and $m_z \in [x,y]$ both located at distance $\alpha_x = (y|z)_x$ from $x$. There is a unique isometry $\varphi$ which maps $\Delta(x,y,z)$ to a tripod $T(x,y,z)$ consisting of three solid segments $[x,m]$, $[y,m]$, and $[z,m]$ of lengths $\alpha_x$, $\alpha_y$, and $\alpha_z$, respectively. This function maps the vertices $x,y,z$ of $\Delta(x,y,z)$ to the respective leaves of $T(x,y,z)$ and the points $m_x$, $m_y$, and $m_z$ to the center $m$ of $T(x,y,z)$. Any other point of $T(x,y,z)$ is the image of exactly two points of $\Delta(x,y,z)$. A geodesic triangle is called $\delta$-thin if for all points $u,v \in \Delta(x,y,z)$, $\varphi(u) = \varphi(v)$ implies $d(u,v) \leq \delta$.

The slimness $sl(X)$ (thinness $th(X)$) of a metric space $X$ is the minimum $\delta$ such that any geodesic triangle of $X$ is $\delta$-slim ($\delta$-thin).

Why they are synonymous

They are comparable because a constant bound on one of $sl(X)$ or $th(X)$ implies a constant bound on the other (and, even other comparable values of hyperbolicity not mentioned here). Specifically, $$sl(X) \le th(X) \le 4sl(X)$$

References

• M.R. Bridson and A. Haefliger, Metric spaces of non-positive curvature, volume 319 of Grundlehren der mathematischen Wissenschaften. Springer-Verlag, Berlin, 1999; DOI: 10.1007/978-3-662-12494-9, see also here.