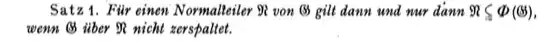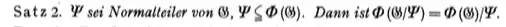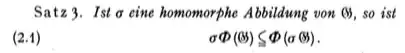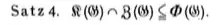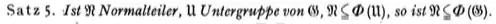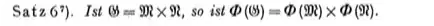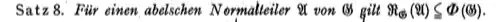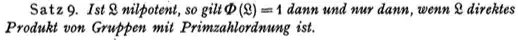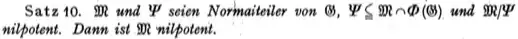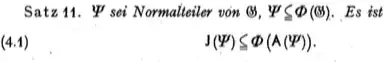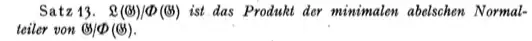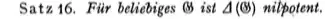Feel free to edit , as I am not about the translation of certain terms and I cannot read german fractura very well. (Perhaps you might also want to leave a comment for saying what you changed and why you changed it.)
I denote the words I was not sure how to translate and comments with questionmarks and $[]$ brackets.
Definitions:
- $A(G)$: the automorphism group of $G$.
- $J(G)$: the group of inner automorphisms of $G$.
- $Z(G)$: the centre of $G$.
- $K(G)$: the commutator subgroup of $G$.
- $L(G)$: the maximal nilpotent subgroup of $G$.
- $\Phi(G)$: the intersection of the maximal subgroups of $G$.
- $\Delta(G)$: the intersection of the maximal and non-invariant subgroups of $G$.
- If $N$ is a normal subgroup of $G$, and $G=N\overline{G}$, where $\overline{G}$ is a subgroup of $G$ and $\overline{G}\subset G$ ($N\cap\overline{G}=1$, resp.), we say that $G$ splits (decomposes, resp.) over $G$.
- If $\Gamma$ is a subgroup of $A(G)$, a group $R$ is $\Gamma$-fully-reducible if $R$ is a product of minimal subgroups of $R$ invariant under $\Gamma$. In particular, if $R$ is a normal subgroup of a group $G$, and $\Gamma$ the group of automorphisms of $R$ induced by transformations by the elements of $G$ [I take this to mean conjugation. -BMS], and $R$ is $\Gamma$-fully-reducible, we say that $R$ is $G$-fully-reducible.
- Let $N$ be an arbitrary normal subgroup of $G$. $S_{G}(N)$ denotes the product of the minimal normal subgroups of $G$ in $N$. $S_{G}(N)$ is the maximal $G$-fully-reducible normal subgroup contained in $N$. We denote by $R_{G}(N)$ the intersection of the normal subgroups of $G$ maximal in $N$. $N/R_{G}(N)$ is $G/R_{G}(N)$-fully-reducible, and $R_{G}(N)$ contains no normal subgroup $M$ of $G$ with $G/M$-fully-reducible factor group $N/M$. We call $S_{G}(G)$ the Sockel of $G$ and write simply $S(G)$.
Theorem 1: Let $N$ be a normal subgroup of $G$. Then $N \subseteq \Phi(G)$ if and only if $G$ does not split over $N$.
Theorem 2: Let $\Psi$ be a normal subgroup of $G$, $\Psi\subseteq \Phi(G)$. Then $\Phi(G/\Psi) = \Phi(G) /\Psi$.
Theorem 3: If $\sigma$ is a homomorphism with domain $G$, then $$(2.1) \qquad\qquad\qquad\qquad\sigma\Phi(G)\subseteq \Phi(\sigma G)\;.$$
Theorem 4: $K(G) \cap Z(G) \subseteq \Phi(G)$.
Theorem 5: If $N$ is a normal supgroup and $U$ a subgroup of $G$, and $N \subseteq \Phi(U)$, then $N \subseteq \Phi(G)$.
Theorem 6). If $G = M \times N$. then $\Phi(G) = \Phi(M) \times \Phi(N)$.
Theorem 7: If $A$ is an Abelian normal subgroup of $G$, and $$(2.5)\qquad\qquad\qquad A \cap \Phi(G) = 1\;,$$ then $G$ decomposes over $A$. Moreover, $A$ is $G$-fully-reducible.
Theorem 8: If $A$ is an Abelian normal subgroup of $G$, then $R_{G}(A) \subseteq \Phi(G)$.
Theorem 9: If $L$ is nilpotent, then $\Phi(L) = 1$ if and only if $L$ is a direct product of groups of prime order.
Theorem 10: Let $M$ and $\Psi$ be normal supgroups of $G$, $\Psi \subseteq M \cap \Phi(G)$ and $M / \Psi$ nilpotent. Then $M$ is nilpotent.
Theorem 11: Let $\Psi$ be a normal supgroup of $G$, $\Psi \subseteq \Phi(G)$. Then $$(4.1)\qquad\qquad\qquad J(\Psi) \subseteq \Phi(A(\Psi))\;.$$
Theorem 12: In a $\Phi$-free group $F$, $L(F)$ is the product of the minimal Abelian normal subgroups of $F$.
Theorem 13: $L(G) / \Phi(G)$ is the product of the minimal Abelian normal subgroups of $G/\Phi(G)$.
Theorem 14: A group is $\Phi$-free if and only if it decomposes over the Abelian component of its Sockel.
Theorem 15: In a $\Phi$-free group $F$,
$$(5.4) \qquad\qquad\qquad Z(F/Z(F)) = Z(F) / Z (F)$$ and
$$(5.5) \qquad \qquad\qquad Z (F) = \Delta(F)\;.$$
Theorem 16: For an arbitrary $G$, $\Delta(G)$ is nilpotent.
Theorem 17: Let $S$ be a direct product of simple groups and $\{\Gamma\}$ a complete system of representatives of the classes of $A(S)$ conjugated subgroups of $A(S)$ with the following properties:
$(I): \quad S_\alpha$ is $\Gamma_\alpha$-fully-reducible
$(II): \quad J(S_\eta) \subseteq \Gamma$
If $\Gamma$ runs through this system of representatives, then the groups $F_\Gamma$ with the elements $(a,\gamma)$, $a\in S_\alpha$, $\gamma \in \Gamma$, and the operation defined by
$$(a,\gamma) (b,\delta) = (ab^{\gamma_\alpha},\gamma \delta)$$
are a complete system of representatives of the types of the $\Phi$-free groups of a Sockel of type $S$.