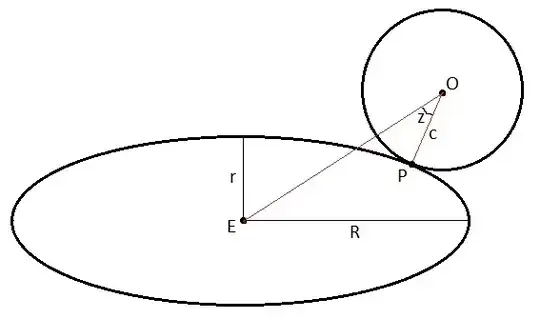
The problem posed is algebraically intractable.
If instead of O you know $P$, then you can find the angle after extending line OP to meet the major axis at $F$.
Label the intersection on the right of the ellipse with its major axis $G$. Let
$\angle GFO$ be $\alpha$ and $\angle GEO$ be $\beta$; then if we can determine $\alpha$ and $\beta$, $\angle z = \alpha - \beta$.
But if the projections of $EP$ along the major and minor axes are $(x,y)$ respectively, then
$$
\tan \alpha = \frac{yR^2}{xr^2}
$$
and
$$
\tan \beta = \frac{y+c\sin\alpha}{x+c \cos \alpha}
$$
Take the respective arctangents and subtract.
For the problem posed, you have $O$ so $\beta$ is trivially $\tan^{-1}\frac{y_0}{x_0}$, but to get $\alpha$ you would need to solve for $x, y, \alpha$ in
the equations
$$
\left\{
\begin{array}{c}
\tan \alpha = \frac{yR^2}{xr^2} \\
x + c \cos \alpha = x_0 \\
y + c \sin \alpha = y_0
\end{array}
\right.
$$
You can use trig identities to eliminate $\alpha$ and solve the last equation for $y$ in terms of $x$, but the remaining equation involves square roots of two expressions, one of which has $(x-x_0)^2$ in a denominator, and when you group and square twice you end out with an 8-th degree equation which is much too tough to solve.