How to calculate $$ \lim_{n\to\infty}(\sin n)^{n} \, ? $$ Is it sufficiently that since $|\sin x|\leq 1$ $\forall x\in\mathbb{R}$ and $|\sin n|<1$ $\forall n\in\mathbb{N}$ then $$ \lim_{n\to\infty}(\sin n)^{n}=0 \, ? $$ Is it true that if $|a_{n}|<1$ $\forall n\in\mathbb{N}$ then $$ \lim_{n\to\infty}(a_{n})^{n}=0 \, ? $$
-
5Your second part is not true. For instance, if $a_n = 1-1/n$, then $a_n^n \to 1/e$. – Adhvaitha Nov 13 '14 at 20:27
-
1It's possible this sequence doesn't even converge. $n \pmod{2\pi}$ is dense in the circle, so the numbers get arbitrarily close to $1$. It's hard to predict how close to $1$ and when though. – Matt Samuel Nov 13 '14 at 20:29
-
$(\sin n)^{n^2}$ diverges as well. – Sungjin Kim Nov 13 '14 at 22:35
2 Answers
This limit does not exist, you can find two distinct accumulation points.
By the theorem of Dirichlet, you will find as many integers $p,q$ as you want such that $$|\pi-\frac pq|<\frac1{q^2},$$or $$|q\pi-p|<\frac1{q}.$$ Taking the sine and raising to the $p^{th}$ power, $$|\sin^pp|<\sin^p\frac1{q},$$ i.e. with $q>\frac p4$, $\color{blue}{\sin^pp}$ is arbitrarily close to $\color{blue}0$ infinitely many times.
For the same reason, you will find as many integers $p,q=2^er$ (odd $r$) as you want such that $$|\frac\pi{2^{e+1}}-\frac pq|<\frac1{q^2},$$or $$|r\frac\pi{2}-p|<\frac1{q}.$$ Taking the cosine (a decreasing function) and raising to the $p^{th}$ power, $$|\sin^pp|>\cos^p\frac1{q},$$ i.e. noting that $q>2^{e-1}p$, $\color{blue}{\sin^pp}$ is arbitrarily close to $\color{blue}1$ infinitely many times (as $\cos\frac1q=1-o\left(\frac1q\right)$).
-
-
+1 very nice! Maybe putting a line at the beginning saying "the limit does not exist because : " or something like that would improve readability though :-) – Ant Nov 13 '14 at 22:06
-
-
Perhaps you can show that every point in $[-1,1]$ is a limit point? Maybe it's even uniformly distributed? Or you can find the distribution law? – orangeskid Nov 13 '14 at 22:12
-
@orangeskid: do you think that rationals can be limit points, the Dirichlet theorem does not hold for them ? I believe that the distribution will be strongly skewed in favor of the small values (isn't the peak width decreasing like the inverse square root of $n$ or so ?) – Nov 14 '14 at 09:06
Numerical calculations strongly suggest that the sequence $(\sin n)^n$ is divergent. Here is the plot of the first million terms:
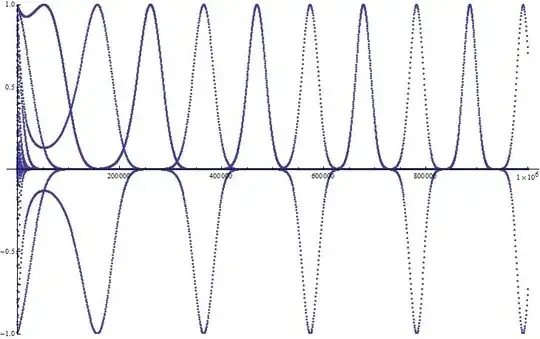
- 20,135
-
There seem to be two graphs, not one. Also, remarkable periodicity. Do you think it has to do with the continued fraction expansion of $\pi$? I am also curious what you used for the calculations. – orangeskid Nov 13 '14 at 22:09
-
@orangeskid I made this plot with Mathematica. There is exactly one point for each value of $n\in{1,2,\ldots,10^6}$. – Spenser Nov 14 '14 at 01:59