This is a generalization of my earlier question here posted recently, and is a more interesting one.
Three consecutive binomial coefficients $$\binom n{r-1},\binom nr, \binom n{r+1}$$ are in an AP (arithmetic progression) with positive common difference. Find possible pairs of $(n, r)$ where both $n, r$ are positive integers.
By scaling the triple we just need that: $$ \frac{r}{n-r+1},1,\frac{n-r}{r+1} $$ are in arithmetic progression, or: $$ r(r+1), (r+1)(n-r+1), (n-r)(n-r+1). $$ This leads to the condition: $$ r(r+1)+(n-r)(n-r+1) = 2(r+1)(n-r+1) $$ that is equivalent to: $$ (2r-n)^2 = n+2.\tag{1} $$ This leads to $n=a^2-2$ and $|2r-n|=a$. Assuming $r\leq\frac{n}{2}$, we get: $$ n=a^2-2,\qquad r=\frac{n-a}{2}=\frac{a^2-a-2}{2}=\frac{(a+1)(a-2)}{2}.\tag{2}$$
I just came across this funny fact while staring at a sufficiently large version of Pascal's triangle that I could see for the first time the arithmetic progression
$${14 \choose 4} = 1001, {14 \choose 5} = 2002, {14 \choose 6} = 3003.$$
This comes from taking $a = 4$ in Jack's parameterization of the solutions. Note also the nice result that in this parameterization the three terms are in the ratio $(a - 2 : a : a + 2)$. So we get the ratio $(2 : 4 : 6) = (1 : 2 : 3)$ above, and also we learn that this ratio never occurs again. For $a = 5$ the solution $(n, r) = (23, 9)$ is in the ratio $(3 : 5 : 7)$, for $a = 6$ the solution $(n, r) = (34, 14)$ is in the ratio $(4 : 6 : 8) = (2 : 3 : 4)$, etc.
Here is a cute connection to the central limit theorem. As we know, the binomial distribution converges to the normal distribution. Here are plots of the binomial distribution for $n = 14$ and for $n = 34$, which corresponds to taking $a = 6$ in Jack's parameterization, see if you can spot the arithmetic progressions:
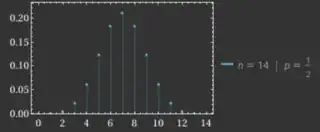
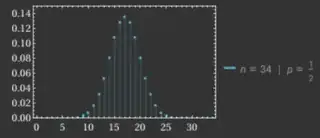
Now, the normal distribution is a curve, the bell curve! And curves are not straight. The bell curve is convex in the tails and concave in the bulk. It is only straight near its inflection points, which you can compute occur at $\mu \pm \sigma$ where $\mu$ is the mean and $\sigma$ is the standard deviation.
What that means is that there's no hope of three consecutive binomial coefficients being in arithmetic progression unless they are next to these inflection points. The binomial distribution with $p = \frac{1}{2}$ has mean $\frac{n}{2}$ and standard deviation $\frac{\sqrt{n}}{2}$, so a solution $(n, r)$ must have the property that $r \approx \frac{n \pm \sqrt{n}}{2}$. And this is what happens here! This gives $|n - 2r| \approx \sqrt{n}$ so in fact $\frac{a}{2}$ is approximately the standard deviation.
Even the ratio $(a - 2 : a : a + 2)$ has an interpretation here; it corresponds to the slope of the normal curve at its inflection points! Namely, this ratio says that the ratio of the rate of change of the binomial distribution to its value is $\frac{2}{a}$ at its inflection points, and for the normal curve $f(x)$ you can check that the value of $\frac{f'(x)}{f(x)}$ at its inflection points is $\frac{1}{\sigma}$.
This suggests a generalization which I've posted as a follow-up question here.
