Subtracting Quarters of Squares Equals Multiply?!

Question

Can anyone explain to me how/why this works (hopefully in mostly layman's terms)?
It seems pretty magical to me at the moment.

$${{(a+b)^2\over4} - {(a-b)^2\over4}} = a b.$$

Answer 1

         

Answer 2

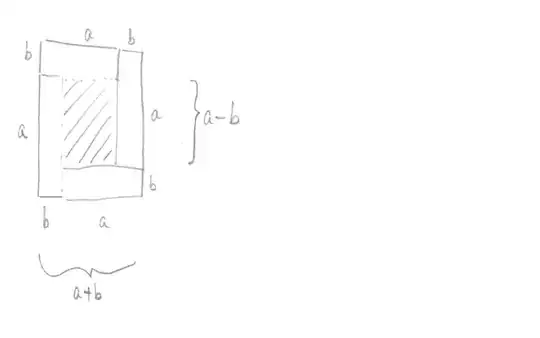
Expanding the squared terms gives \begin{equation} \frac{(a + b)^2}{4} - \frac{(a - b)^2}{4} = \frac{a^2 + 2ab + b^2}{4} - \frac{a^2 - 2ab + b^2}{4} = \frac{4ab}{4} = ab. \end{equation}

Answer 3

In addition to the direct derivations already shown, your magical equation is closely related to the formula $$x^2 - y^2 = (x + y)(x - y).$$ Just set $a = x + y$ and $b = x - y.$ Then $\frac{a+b}2 = x$ and $\frac{a-b}2 = y,$ so $x^2 = \frac{(a+b)^2}4$ and $y^2 = \frac{(a-b)^2}4.$ Use these facts to replace $x^2,\ y^2,\ x + y,$ and $x - y$ in the equation above and you will have derived your magical equation in $a$ and $b.$

Answer 4

Your expression is equal to $\dfrac{a^2+2ab+b^2-a^2+2ab-b^2}{4}=\dfrac{4ab}{4}=ab$

Answer 5

Try writing the fractions $\frac{(a+b)^2}{4}$ and $\frac{(a-b)^2}{4}$ as one, and expanding the brackets. See what happens then.

Answer 6

An underrated way to show identities is to use the fact that if $A-B=0$ then $A=B$:

$$\begin{align*} &\ \frac14(a+b)^2-\frac14(a-b)^2-ab\\[3mm] =&\ \frac14(a^2+2ab+b^2)-\frac14(a^2-2ab+b^2)-ab\\[3mm] =&\ \frac14a^2-\frac14a^2+\frac12ab+\frac12ab+\frac14b^2-\frac14b^2-ab\\[3mm] =&\ ab-ab\\[3mm] =&\ 0 \end{align*}$$

Answer 7

Here's a really detailed step by step proof, suitable for elementary or secondary school students:

$$ \begin{align} \frac{(a+b)^2}{4}-\frac{(a-b)^2}{4}&=ab\\\\(a+b)^2 - (a-b)^2&=4ab\\\\a^2 + 2ab + b^2 - (a^2 - 2ab + b^2)&=4ab\\\\a^2 + 2ab + b^2 - a^2 + 2ab - b^2 &= 4ab\\\\(a^2 - a^2) + (b^2 - b^2) +2ab + 2ab &= 4ab\\\\4ab &= 4ab \end{align} $$