I have found this in a book:
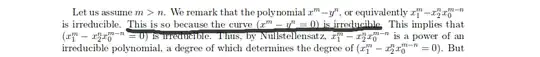
but I don't know why the curve $x^m-y^n=0$ is irreducible when n, m are coprimes.
Can someone help me?
I have found this in a book:
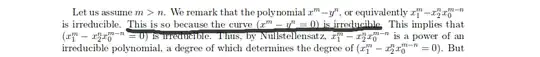
but I don't know why the curve $x^m-y^n=0$ is irreducible when n, m are coprimes.
Can someone help me?
Here's one way to see it. There may be cleaner ones, but this has the advantage of being a brute-force approach that doesn't require any cleverness or special machinery.
Consider the ring $R := k[x, y] / (x^m - y^n) = k[x, \sqrt[n]{x^m}]$. We want to show that $R$ is an integral domain, because this is equivalent to $(x^m - y^n)$ being prime, which is equivalent to the curve $x^m - y^n = 0$ being irreducible.
A general element of $R$ looks like
$$p_0(x) + p_1(x) \sqrt[n]{x^m} + p_2(x) \left(\sqrt[n]{x^m}\right)^2 + \cdots + p_{n-1}(x) \left(\sqrt[n]{x^m}\right)^{n-1}$$
where the $p_i$ are polynomials, and moreover this representation is unique. (For uniqueness, we're using that $m, n$ are relatively prime).
So, take another element, say
$$q_0(x) + q_1(x) \sqrt[n]{x^m} + q_2(x) \left(\sqrt[n]{x^m}\right)^2 + \cdots + q_{n-1}(x) \left(\sqrt[n]{x^m}\right)^{n-1},$$
multiply them together, and show that if you get zero from this then either all the $p_i$ were zero or all the $q_i$ were zero.