Getting vague results using VAR time series forecasting in python!

Question

Firstly, I am a beginner in this field of Data Science and have tried to implement some time series models for wind speed forecasting. Also, I am aware of the fact that some regression models might give better results, but still, my aim is to crack the same with the help of VAR

I tried to implement multivariate time series forecasting - VAR in python. To start with I followed the code in this article- https://towardsdatascience.com/simple-multivariate-time-series-forecasting-7fa0e05579b2

However, the forecasted value for my dataset is vague and I am unable to figure out why is the case! Anyone who can help me figure out the possible dent/mistake in the code and hopefully a solution for the same will be appreciated.

PS: I also want to know that how can one get MSE or RMSE or residual terms for each forecasted value in the form of single-column array/vector instead of a single overall error value?

    # Importing libraries
      import numpy as np
import pandas as pd
import matplotlib.pyplot as plt, seaborn as sb
Importing Dataset
df =  pd.read_csv("/Users/NEILYUG/Documents/ws_TN.csv")
ds = df.drop(['samples'], axis = 1)
Visualize the trends in data
sb.set_style('darkgrid')
ds.plot(kind = 'line', legend = 'reverse', title = 'Visualizing Sensor Array Time-Series')
plt.legend(loc = 'upper right', shadow = True, bbox_to_anchor = (1.35, 0.8))
plt.show()
Dropping Temperature & Relative Humidity as they do not change with Time
ds.drop(['Pressure','Temperature'], axis = 1, inplace = True)
Again Visualizing the time-series data
sb.set_style('darkgrid')
ds.plot(kind = 'line', legend = 'reverse', title = 'Visualizing Sensor Array Time-Series')
plt.legend(loc = 'upper right', shadow = True, bbox_to_anchor = (1.35, 0.8))
plt.show()

    # Splitting the dataset into train & test subsets
    n_obs = 892
    ds_train, ds_test = ds[:-n_obs], ds[-n_obs:]
# Augmented Dickey-Fuller Test (ADF Test) to check for stationarity
from statsmodels.tsa.stattools import adfuller

def adf_test(ds):
    dftest = adfuller(ds, autolag='AIC')
    adf = pd.Series(dftest[0:4], index = ['Test Statistic','p-value','# Lags','# Observations'])

    for key, value in dftest[4].items():
       adf['Critical Value (%s)'%key] = value
    print (adf)

    p = adf['p-value']
    if p &lt;= 0.05:
        print(&quot;\nSeries is Stationary&quot;)
    else:
        print(&quot;\nSeries is Non-Stationary&quot;)


for i in ds_train.columns:
    print(&quot;Column: &quot;,i)
    print('--------------------------------------')
    adf_test(ds_train[i])
    print('\n')

# Differencing all variables to get rid of Stationarity
ds_differenced = ds_train.diff().dropna()

# Running the ADF test once again to test for Stationarity
for i in ds_differenced.columns:
    print(&quot;Column: &quot;,i)
    print('--------------------------------------')
    adf_test(ds_differenced[i])
    print('\n')

# Now cols: 3, 5, 6, 8 are non-stationary
ds_differenced = ds_differenced.diff().dropna()

# Running the ADF test for the 3rd time to test for Stationarity
for i in ds_differenced.columns:
    print(&quot;Column: &quot;,i)
    print('--------------------------------------')
    adf_test(ds_differenced[i])
    print('\n')


from statsmodels.tsa.api import VAR

model = VAR(ds_differenced)
results = model.fit(maxlags = 15, ic = 'aic')
results.summary()

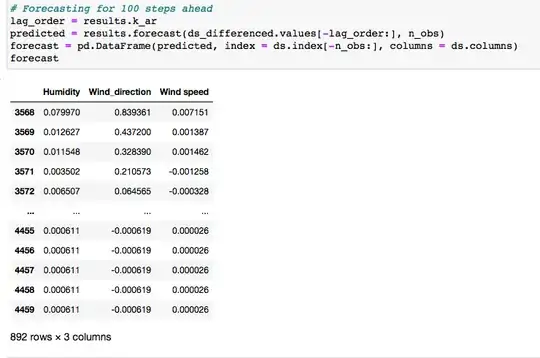
Forecasting for 100 steps ahead
lag_order = results.k_ar
predicted = results.forecast(ds_differenced.values[-lag_order:], n_obs)
forecast = pd.DataFrame(predicted, index = ds.index[-n_obs:], columns = ds.columns)

Plotting the Forecasted values
p1 = results.plot_forecast(1)
p1.tight_layout()

Inverting the Differencing Transformation
def invert_transformation(ds, df_forecast, second_diff=False):
    for col in ds.columns:
        # Undo the 2nd Differencing
        if second_diff:
            df_forecast[str(col)] = (ds[col].iloc[-1] - ds[col].iloc[-2]) + df_forecast[str(col)].cumsum()

        # Undo the 1st Differencing
        df_forecast[str(col)] = ds[col].iloc[-1] + df_forecast[str(col)].cumsum()

    return df_forecast

forecast_values = invert_transformation(ds_train, forecast, second_diff=True)

======================================   Visualization  ==========================================
Actual vs Forecasted Plots
fig, axes = plt.subplots(nrows = int(len(ds.columns)/2), ncols = 2, dpi = 100, figsize = (10,10))

for i, (col,ax) in enumerate(zip(ds.columns, axes.flatten())):
    forecast_values[col].plot(color = 'r', legend = True, ax = ax).autoscale(axis =' x',tight = True)
    ds_test[col].plot(color = 'b', legend = True, ax = ax)

    ax.set_title('Sensor: ' + col + ' - Actual vs Forecast')
    ax.xaxis.set_ticks_position('none')
    ax.yaxis.set_ticks_position('none')

    ax.spines["top"].set_alpha(0)
    ax.tick_params(labelsize = 6)

plt.tight_layout()
plt.savefig('actual_forecast.png')
plt.show()

MSE
from sklearn.metrics import mean_squared_error
from numpy import asarray as arr
mse = mean_squared_error(ds_test, forecast_values)

the orange line is predicted value and it is clearly out of my understanding

the forecasted values:

Getting vague results using VAR time series forecasting in python!

Importing Dataset

Visualize the trends in data

Dropping Temperature & Relative Humidity as they do not change with Time

Again Visualizing the time-series data

Forecasting for 100 steps ahead

Plotting the Forecasted values

Inverting the Differencing Transformation

====================================== Visualization ==========================================

Actual vs Forecasted Plots

MSE

0 Answers0