Decision tree with final decision being a linear regression

Question

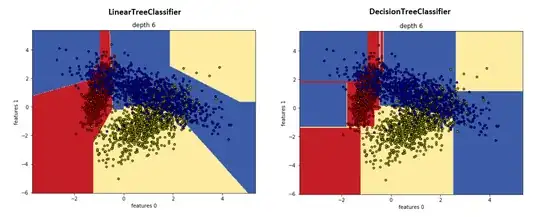
Question: I want to implement a decision tree with each leaf being a linear regression, does such a model exist (preferable in sklearn)?

Example case 1:

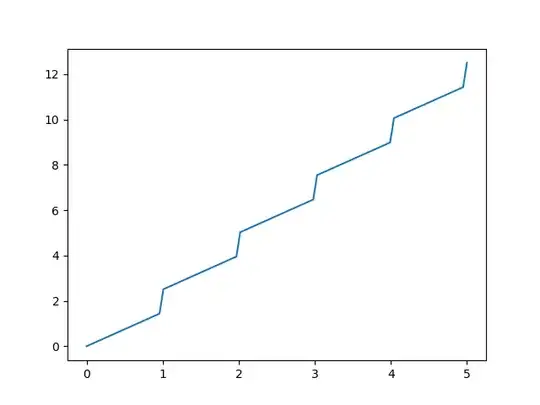
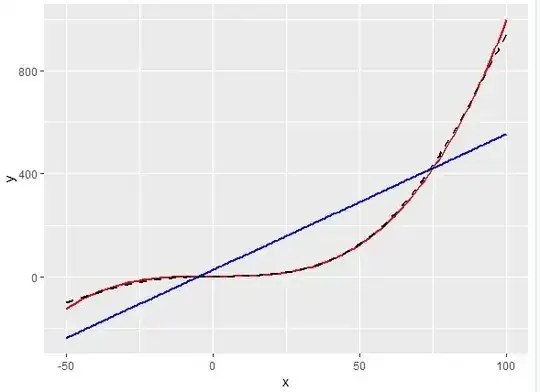
Mockup data is generated using the formula:

y = int(x) + x * 1.5

Which looks like:

I want to solve this using a decision tree where the final decision results in a linear formula. Something like:

1. 0 <= x < 1 -> y = 0 + 1.5 * x
2. 1 <= x < 2 -> y = 1 + 1.5 * x
3. 2 <= x < 3 -> y = 2 + 1.5 * x
4. etc.

Which I figured could best be done using a decision tree. I've done some googling and I thought the DecisionTreeRegressor from sklearn.tree could work, but that results in points being assigned a constant value in a range, as shown below:

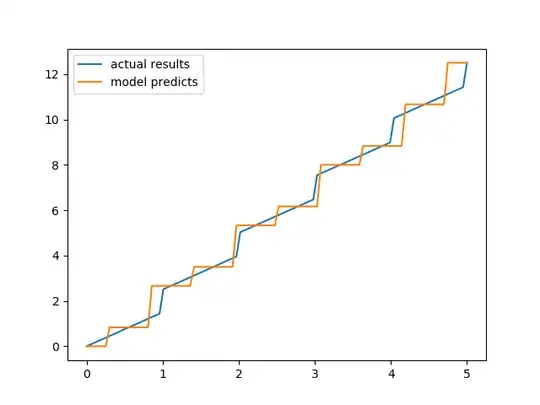
Code:

import matplotlib.pyplot as plt
import numpy as np
from sklearn.tree import DecisionTreeRegressor

x = np.linspace(0, 5, 100)
y = np.array([int(i) for i in x]) + x * 1.5

x_train = np.linspace(0, 5, 10)
y_train = np.array([int(i) for i in x_train]) + x_train * 1.5

clf = DecisionTreeRegressor()
clf.fit(x_train.reshape((len(x_train), 1)), y_train.reshape((len(x_train), 1)))

y_result = clf.predict(x.reshape(len(x), 1))
plt.plot(x, y, label='actual results')
plt.plot(x, y_result, label='model predicts')
plt.legend()
plt.show()

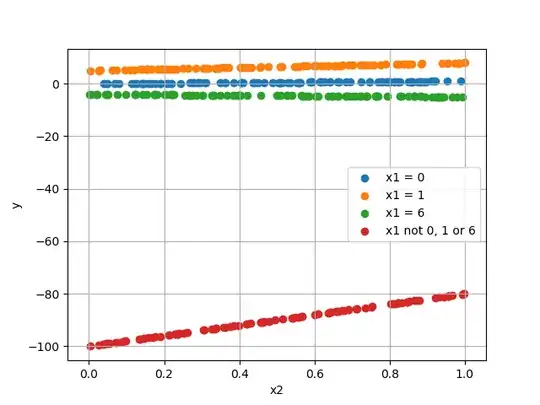
Example case 2: Instead of one input, there are two inputs: x1 and x2, output is computed by:

1. x1 = 0 -> y = 1 * x2
2. x1 = 1 -> y = 3 * x2 + 5
3. x1 = 6 -> y = -1 * x2 -4
4. else -> y = x2 * 20 - 100

Code:

import matplotlib.pyplot as plt
import random

def get_y(x1, x2):
    if x1 == 0:
        return x2
    if x1 == 1:
        return 3 * x2 + 5
    if x1 == 6:
        return - x2 - 4
    return x2 * 20 - 100

X_0 = [(0, random.random()) for _ in range(100)]
x2_0 = [i[1] for i in X_0]
y_0 = [get_y(i[0], i[1]) for i in X_0]
X_1 = [(1, random.random()) for _ in range(100)]
x2_1 = [i[1] for i in X_1]
y_1 = [get_y(i[0], i[1]) for i in X_1]
X_2 = [(6, random.random()) for _ in range(100)]
x2_2 = [i[1] for i in X_2]
y_2 = [get_y(i[0], i[1]) for i in X_2]
X_3 = [(random.randint(10, 100), random.random()) for _ in range(100)]
x2_3 = [i[1] for i in X_3]
y_3 = [get_y(i[0], i[1]) for i in X_3]
plt.scatter(x2_0, y_0, label='x1 = 0')
plt.scatter(x2_1, y_1, label='x1 = 1')
plt.scatter(x2_2, y_2, label='x1 = 6')
plt.scatter(x2_3, y_3, label='x1 not 0, 1 or 6')
plt.grid()
plt.xlabel('x2')
plt.ylabel('y')
plt.legend()
plt.show()

So my question is: does a decision tree with each leaf being a linear regression, exist?

Answer 1

I think the easiest way to do this would be to have a decision tree where the final decision results in a linear formula.

Setting aside whether this is actually easiest/best, this type of model does exist, usually called "model-based recursive partitioning". See e.g. https://stats.stackexchange.com/q/78563/232706
There are several packages in R for this: partyfit (and the older simpler party), mob, Cubist; unfortunately, there don't seem to be any in Python yet. Here's a discussion on including it in sklearn, from mid-2018.

Answer 2

You are looking for Linear Trees.

Linear Trees differ from Decision Trees because they compute linear approximation (instead of constant ones) fitting simple Linear Models in the leaves.

For a project of mine, I developed linear-tree: a python library to build Model Trees with Linear Models at the leaves.

linear-tree is developed to be fully integrable with scikit-learn.

from sklearn.linear_model import *
from lineartree import LinearTreeRegressor, LinearTreeClassifier
REGRESSION
regr = LinearTreeRegressor(base_estimator=LinearRegression())
regr.fit(X, y)
CLASSIFICATION
clf = LinearTreeClassifier(base_estimator=RidgeClassifier())
clf.fit(X, y)

LinearTreeRegressor and LinearTreeClassifier are provided as scikit-learn BaseEstimator. They are wrappers that build a decision tree on the data fitting a linear estimator from sklearn.linear_model. All the models available in sklearn.linear_model can be used as linear estimators.

Compare Decision Tree with Linear Tree:

Answer 3

I would suggest using spline regression. or some polynomial regression.

Why? what you are basically approximating is the (almost) step-wise function. See here

More info in here and a great background introduction in here.

Answer 4

Even after your update, I think Noah's hint to spline regression is the best way to approach the problem. Here is a brief example in R:

# Generate data
x <- -50:100
y <- 0.001*x^3
plot(x,y)
df = data.frame(y,x)

# Linear regression
reg_ols=lm(y~.,data=df)
pred_ols = predict(reg_ols, newdata=df)

# GAM with regression splines
library(gam)
reg_gam = gam(y~s(x,5), data=df)
pred_gam = predict(reg_gam, newdata=df)

# Plot prediction and actual data
require(ggplot2)
df2 = data.frame(x,y,pred_ols, pred_gam)
ggplot(df2, aes(x)) +                    
  geom_line(aes(y=y),size=1, colour="red") +  
  geom_line(aes(y=pred_ols),size=1, colour="blue") +
  geom_line(aes(y=pred_gam),size=1, colour="black", linetype = "dashed")  

So I have some function which is the data generating process (red line in the plot) and I want to get a good fit on this function. OLS (linear regression) will not work well (blue line in plot) but a GAM with splines will fit very well (black dashed).

This model looks like $y_i=\beta_0 + \beta_1 x_{1,i} + u_i$ (so 2D-like), but of course you can expand the model to $y_i=\beta_0 + \beta_1 x_{1,i} + ... + \beta_k x_{k,i} + u_i$, where $k$ is the number of "variables" in the model (so kD-like).

Since you seem to be on Python, you would need to look for a Py implementation of GAMs, such as Statsmodels of PyGAM.

Chapter 7 of "Introduction to Statistical Learning" covers splines regression. You may have a look at the Python Lab for the book.

Answer 5

Create a new column based on your formula and train your decision tree. Then, based on the outcome class of the tree, pass the data to different regression.

This would be a sort of Stacking.

Please treat this just an engineering approach, it might not be a good solution based on your data and need.