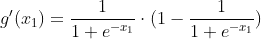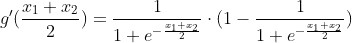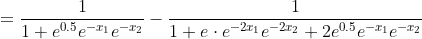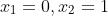Why is taking the gradient of the average error in SGD not correct, but rather the average of the gradients of single errors?

Question

I am a little confused about taking averages in cost functions and SGD. So far I always thought in SGD you would compute the average error for a batch and then backpropagate it. But then I was told in a comment on this question that that was wrong. You need to backpropagate the error of every item in the batch individually, then average the gradients you computed through the backpropagation and then update your parameters with the scaled average gradient.

Okay, but why is that not actually the same thing? Isn't the gradient of the average of some points the average of the gradient at these points?

The idea behind SVD is to find the minimum of a cost function $J(\theta)$ of a subset of training items. The cost function is usually defined as the average of some function $J_t(\theta)$ of the errors of the individual predictions and targets for a training item. Let's take MSE as an example. So if we have a batch of $N$ items, we have

$$J(\theta) : X, Y \mapsto \frac{1}{N} \sum_{i=1}^N (y_i -f(x_i))^2$$

And we want to minimize $J(\theta)$. So we need to find its gradient:

$$\nabla \frac{1}{n}\sum_{i=1}^{n} (y_i - f(x_i))^2$$

But the derivative is linear, so

$$\nabla \frac{1}{n}\sum_{i=1}^{n} (y_i - f(x_i))^2 = \frac{1}{n}\sum_{i=1}^{n} \nabla (y_i - f(x_i))^2$$

What am I doing wrong here?

Another example. Say we do linear regression with an $m x + b$ line fit. Then the partial derivatives taken for $m$ and $b$ are

\begin{align*} \frac{\partial J(\theta)}{\partial m} &= \frac{1}{N} \frac{\partial}{\partial m} \sum_{i=1}^N (y_i -f(x_i))^2 & \texttt{factor rule}\\ &= \frac{1}{N} \sum_{i=1}^N \frac{\partial}{\partial m} (y_i -f(x_i))^2 & \texttt{sum rule}\\ &= \frac{1}{N} \sum_{i=1}^N 2(y_i -f(x_i)) \frac{\partial}{\partial m} y_i -f(x_i) & \texttt{chain rule}\\ &= \frac{1}{N} \sum_{i=1}^N 2(y_i -f(x_i)) \frac{\partial}{\partial m} y_i - (mx_i + b) & \texttt{definition } f\\ &= \frac{1}{N} \sum_{i=1}^N 2(y_i -f(x_i)) (-x_i) & \texttt{}\\ &= -\frac{2}{N} \sum_{i=1}^N x_i(y_i -f(x_i)) & \texttt{comm., distr.}\\ \end{align*}

\begin{align*} \frac{\partial J(\theta)}{\partial b} &= \frac{1}{N} \frac{\partial}{\partial b} \sum_{i=1}^N (y_i -f(x_i))^2 & \texttt{factor rule}\\ &= \frac{1}{N} \sum_{i=1}^N \frac{\partial}{\partial b} (y_i -f(x_i))^2 & \texttt{sum rule}\\ &= \frac{1}{N} \sum_{i=1}^N 2(y_i -f(x_i)) \frac{\partial}{\partial b} y_i -f(x_i) & \texttt{chain rule}\\ &= \frac{1}{N} \sum_{i=1}^N 2(y_i -f(x_i)) \frac{\partial}{\partial b} y_i - (mx_i + b) & \texttt{definition } f\\ &= \frac{1}{N} \sum_{i=1}^N 2(y_i -f(x_i)) (-1) & \texttt{}\\ &= -\frac{2}{N} \sum_{i=1}^N (y_i -f(x_i)) & \texttt{comm., distr.}\\ \end{align*}

I don't see an error here and the gradient descent also works with these partial derivatives (tested through implementation). So... what am I missing?

Answer 1

The gradient of the average error doesn't always equal to the average gradient of errors. The source for the difference between them lies in the non-linear layers of the model.

Example:

You can easily see it in the following example with the gradient of the sigmoid function:

The sigmoid function is defined as:

It has a very convenient derivative:

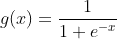
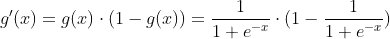
We now take 2 inputs and calculate the mean of the sigmoid's gradient with respect to them:

We now calculate the sigmoid's gradient with respect to their mean:

These 2 results are clearly not the same. If you want further proof, just calculate the numerical results for:

You will get that the mean gradient is ~0.2233, and the gradient of means is ~0.235.

Answer 2

Why is taking the gradient of the average error in SGD not correct,

It is correct.

but rather the average of the gradients of single errors?

You are mis-quoting the original comments. This your original comment:

In an MLP first averaging the error of the entire batch and then calculating the gradient on that average error is identical to calculating the gradient per item and then adjusting the parameters by the average gradient*learning rate, right?

Specifically this is about process. You are looking for a way to take one initial sum before back propagation, not having to back propagate individual gradient calculations, and somehow get the gradient $\nabla J(\theta)$ In other words, you are looking for some equation:

$$\nabla J(\theta) = g(J(\theta))$$

where $g()$ is a function that does not include a sum over individual items. More specifically, it can include a sum over the data items as a constant, but any such sum should not vary with $\theta$.

However, your own calculations show that you do indeed need to back propagate over individual gradients, because $2(y_i - f(x_i))x_i$ is the gradient of a single term of $J(\theta)$ w.r.t. the data set and includes the value of $\theta$ in $f(x_i) = mx_i+b$, where your $m$ and $b$ are the two components of $\theta$ that you want to calculate the gradient over.

This is unavoidable - to calculate $\nabla J(\theta)$ you need to calculate and sum the individual terms of $\sum_i \nabla \mathcal{L}(y_i, x_i, \theta)$ where $\mathcal{L}()$ is your loss function, and you cannot move your sums inside that loss function because $\nabla \mathcal{L}(\frac{y_1 + y_2}{2}, \frac{x_1 + x_2}{2}, \theta) \neq \nabla \frac{1}{2}(\mathcal{L}(y_1, x_1, \theta) + \mathcal{L}(y_2, x_2, \theta))$ nor are there any similar relationships that hold true on aggregating parameters of $\mathcal{L}$ in general that would allow you to work with a pre-calculated sum of losses and a non-linear loss function, then somehow calculate the correct gradient.

If you could remove $\sum_i$ from the right hand side and re-write it in terms of $J(\theta)$ plus some general derivative of the cost function then you would have found a way to feed just the average error into a back propagation routine and obtain $\nabla J(\theta)$ from $J(\theta)$.

If your cost function is simply linear you can resolve this and create something that works. Here to keep the example simple, $\theta$ is just a single real value, and the "partial" derivative just a plain derivative, but the main difference is not using squared error:

$$J(\theta) = \frac{1}{N} \sum_i (y_i - \theta x_i)$$

Then

$$\nabla J(\theta) = \frac{1}{N} \nabla \sum_i (y_i - \theta x_i)$$

$$= \frac{1}{N} \sum_i \nabla (y_i - \theta x_i)$$

$$= \frac{1}{N} \sum_i -x_i$$

whilst this is a still a sum over $i$, it is independent of $\theta$, so you can pre-calculate $\frac{1}{N} \sum_i -x_i$ on a first iteration and treat it like a constant on all further iterations. Technically this meets the requirement above that $\nabla J(\theta) = g(J(\theta))$ where $g(z) = 0z + K$ ($z$ is just the parameter of $g()$ and $K$ is a constant).

This also tells you as an aside that:

• there is no global minimum for the given error function $J(\theta) = \frac{1}{N} \sum_i (y_i - \theta x_i)$. Assuming this constant is non-zero, you can always reduce $J(\theta)$ by changing $\theta$

• you need the derivative of the cost function to depend on its parameters in order to talk meaningfully about optimising those parameters.

It is harder to construct an error function where you did get some non-trivial function of $J(\theta)$ in the right hand side, and no sums over $i$ involving individual gradient calculations. I could not think of a way to do it offhand, but it could be possible. The chances of this being a useful objective function for minimisation seem low though.

I have not mentioned neural network back propagation so far in the above argument, because I wanted to show that the flaw in the thinking applies whenever there is a non-linear function to back propagate over. This even happens using MSE with linear regression. However in a neural network, the same issue occurs at each and every layer where there is a non-linear function (including the error gradient).

It is common to set up a neural network with a simple error gradient for the first layer by combining output transfer function with an objective function so that the initial gradient looks simple. Often literally just the difference between prediction and ground truth $\hat{y}_i - y_i$. You may be thinking that you can average this gradient, then perform the rest of back propagation with it. You cannot, for a similar reason as outlined above, but using the back propagation relations between layers instead of the loss functions. The argument is the same, there is no $\nabla_{W^l} J = g(\nabla_{W^{l+1}} J)$ where $g()$ does not involve a sum over all the individual gradients due to data items from $W^{l+1}$.