In a Transformer model, why does one sum positional encoding to the embedding rather than concatenate it?

Question

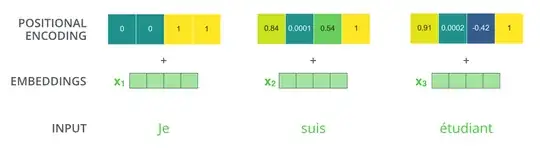
While reviewing the Transformer architecture, I realized something I didn't expect, which is that :

• the positional encoding is summed to the word embeddings
• rather than concatenated to it.

http://jalammar.github.io/images/t/transformer_positional_encoding_example.png

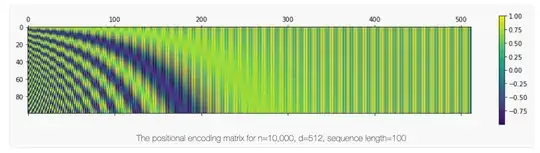
Based on the graphs I have seen wrt what the encoding looks like, that means that :

• the first few bits of the embedding are completely unusable by the network because the position encoding will distort them a lot,
• while there is also a large amount of positions in the embedding that are only slightly affected by the positional encoding (when you move further towards the end).

https://www.tensorflow.org/beta/tutorials/text/transformer_files/output_1kLCla68EloE_1.png

So, why not instead have smaller word embeddings (reduce memory usage) and a smaller positional encoding retaining only the most important bits of the encoding, and instead of summing the positional encoding of words keep it concatenated to word embeddings?

Answer 1

When you concatenate, you have to define a priori the size of each vector to be concatenated. This means that, if we were to concatenate the token embedding and the positional embedding, we would have to define two dimensionalities, $d_t$ for the token and $d_p$ for the position, with the total dimensionality $d = d_t + d_p$, so $d>d_t$ and $d>d_p$. We would be decreasing the total size we devote to tokens in favor of positional information.

However, adding them together is potentially a super case of the concatenation: imagine that there is an ideal split of $d$ into $d_t$ and $d_p$ in terms of minimizing the loss; then, the training could converge to position vectors that only take $d_t$ elements, making the rest zero, and the positions were learned and happened the same, taking the complementary $d_p$ elements and leaving the rest to zero.

Therefore, by adding them, we leave the optimization of the use of the $d$ dimensions to the optimization process, instead of assuming there is an optimal partition of the vector components and setting a new hyperparameter to tune. Also, the use of the vector space is not restricted by a hard split in the vector components, but takes the whole representation space.

Answer 2

the first few bits of the embedding are completely unusable by the network because the position encoding will distort them a lot

This confused me very much at first because I was thinking of the model using a pre-trained word embedding. And then an arbitrary initial chunk of that embedding gets severely tampered with by the positional encoding.

However, in the original transformer model at least, the embedding was trained from scratch, so this does not apply. An initial chunk of the overall embedding will be used for positional information, and the rest will be used for word information.

This still doesn't explain why we use this method instead of concatenation -- see the other answers for that -- but it does explain why the method isn't crazy.

That said, it may be that the method works well even with pre-trained word embeddings, I don't know. If so, it's hard to explain.

Answer 3

The confusion here is that we believe positional embedding is a more complicated version of adding positional information to the word embedding; however, it is not actually. Adding new dimensions to each embedding increases the dimensionality of the problem. On the other hand, please note that the added positional embedding is (almost) static, as shown in this image for a 2D positional embedding:

The added positional embeddings are the same for all the inputs, and the transformer can separate the positional information from the actual word embedding through the training process. Therefore, the positional embedding doesn't mess with the word embedding information, and adding them is a more efficient way of adding the positional information that concatenates them.

Answer 4

The following is conjecture, not fact.

If you look at how much each scalar in the the positional embedding vector changes as a function of position... you'll find that many of the scalars barely change at all. You can visualize this with any positional embedding plot, where the x axis is usually the [512] length of the vector, and the y axis is the position of the token.

For example, this image is from Jay Alammar's well regarded "The Illustrated Transformer"

Let's try to do this mathematically as well. The implementation of PE's that Jay references is at this Google GitHub repo:

https://github.com/tensorflow/tensor2tensor/tree/23bd23b9830059fbc349381b70d9429b5c40a139

Running the function on a PE/WE of length 512 and max sentence length of 128, let's look at how much the final value in the vector actually changes from the first position, to the 64th position, to the final position. Answer: not much.

print(signal[0, 0, -1])
print(signal[0, 63, -1])
print(signal[0, 127, -1])
tf.Tensor(1.0, shape=(), dtype=float32)
tf.Tensor(0.99998015, shape=(), dtype=float32)
tf.Tensor(0.99991935, shape=(), dtype=float32)

Ditto for a value 16 steps away from the final location:

print(signal[0, 0, -16])
print(signal[0, 63, -16])
print(signal[0, 127, -16])
tf.Tensor(1.0, shape=(), dtype=float32)
tf.Tensor(0.9984067, shape=(), dtype=float32)
tf.Tensor(0.9935305, shape=(), dtype=float32)

I saw elsewhere that BERT's WEs are typically roughly the range of [-2, 2], so adding a 0.007 delta from the PE would not move the WE very much at the -16th position.

So what I think is probably happening is that only ~256 of the PE vector's values are actually moving around as a function of the position... the rest are ~constant. Then the learned WE (Transformers don't use prelearned WE like word2vec or glove), figures out to only use the other ~256 elements. So really... it's conceptually a concat.

notebook here

https://colab.research.google.com/drive/14RGALTsPIYGAuIByXGutK-aYN-PikWzF

Answer 5

The best answer I have seen is this Reddit answer by pappypapaya:

In attention, we basically take two word embeddings (x and y), pass one through a Query transformation matrix (Q) and the second through a Key transformation matrix (K), and compare how similar the resulting query and key vectors are by their dot product. So, basically, we want the dot product between Qx and Ky, which we write as:

(Qx)'(Ky) = x' (Q'Ky).

So equivalently we just need to learn one joint Query-Key transformation (Q'K) that transform the secondary inputs y into a new space in which we can compare x.

By adding positional encodings e and f to x and y, respectively, we essentially change the dot product to

(Q(x+e))' (K(y+f)) = 
(Qx+Qe)' (Ky+Kf) = 
(Qx)' Ky + (Qx)' Kf + (Qe)' Ky + (Qe)' Kf = 
x' (Q'Ky) + x' (Q'Kf) + e' (Q'Ky) + e' (Q'K f) 

where in addition to the original x' (Q'Ky) term, which asks the question "how much attention should we pay to word x given word y", we also have x'(Q'Kf) + e'(Q'Ky) + e'(Q'K f), which ask the additional questions, "how much attention should we pay to word x given the position f of word y", "how much attention should we pay to y given the position e of word x", and "how much attention should we pay to the position e of word x given the position f of word y".

Essentially, the learned transformation matrix Q'K with positional encodings has to do all four of these tasks simultaneously. This is the part that may appear inefficient, since intuitively, there should be a trade-off in the ability of Q'K to do four tasks simultaneously and well.

HOWEVER, MY GUESS is that there isn't actually a trade-off when we force Q'K to do all four of these tasks, because of some approximate orthogonality condition that is satisfied of in high dimensions. The intuition for this is that randomly chosen vectors in high dimensions are almost always approximately orthogonal. There's no reason to think that the word vectors and position encoding vectors are related in any way. If the word embeddings form a smaller dimensional subspace and the positional encodings form another smaller dimensional subspace, then perhaps the two subspaces themselves are approximately orthogonal, so presumably these subspaces can be transformed approx. independently through the same learned Q'K transformation (since they basically exist on different axes in high dimensional space). I don't know if this is true, but it seems intuitively possible.

If true, this would explain why adding positional encodings, instead of concatenation, is essentially fine. Concatenation would ensure that the positional dimensions are orthogonal to the word dimensions, but my guess is that, because these embedding spaces are so high dimensional, you can get approximate orthogonality for free even when adding, without the costs of concatenation (many more parameters to learn). Adding layers would only help with this, by allowing for nonlinearities.

We also ultimately want e and f to behave in some nice ways, so that there's some kind of "closeness" in the vector representation with respect to small changes in positions. The sin and cos representation is nice since nearby positions have high similarity in their positional encodings, which may make it easier to learn transformations that "preserve" this desired closeness.

(Maybe I'm wrong, and the approximate orthogonality arises from stacking multiple layers or non-linearities in the fully-connected parts of the transformer).

tl;dr: It is intuitively possible that, in high dimensions, the word vectors form a smaller dimensional subspace within the full embedding space, and the positional vectors form a different smaller dimensional subspace approximately orthogonal to the one spanned by word vectors. Thus despite vector addition, the two subspaces can be manipulated essentially independently of each other by some single learned transformation. Thus, concatenation doesn't add much, but greatly increases cost in terms of parameters to learn.

Answer 6

It is been a while, but I think anyone ending up here might also be interested in the reading of the following paper:

What Do Position Embeddings Learn? An Empirical Study of Pre-Trained Language Model Positional Encoding (Yu-An Wang, Yun-Nung Chen)

https://www.aclweb.org/anthology/2020.emnlp-main.555

I am not changing the accepted answer as this article is not specific.

Answer 7

Why everyone compares RNN and Transformers, when you should actually compare Feedforward Neural Networks with Transformers? I am really sorry, I cannot comment @shepan6 answer, so I will post an answer.

This means that, so far, transformers do not have any notion of word ordering. - @shepan6

This is totally wrong and misleading. Transformers are just FNNs. Order of input matter. Please stop spreading disinformation. I know two ablation studies about positional encoding - one in "Attention is all you need" [arxiv:1706.03762] and the other in "Convolutional Sequence to Sequence Learning" [arxiv:1705.03122]. Both authors conclude that there is no or negligible difference in performance of 1) different positional encoding; and 2) present/missing positional encoding.

From paper "Attention is all you need":

We also experimented with using learned positional embeddings [9] instead, and found that the two versions produced nearly identical results (see Table 3 row (E)).

From paper "Convolutional Sequence to Sequence Learning":

Table 4 shows that position embeddings are helpful but that our model still performs well without them.

Answer 8

So the question is about why positional embeddings are directly added to word embeddings instead of concatenated. This is a particularly interesting question. To answer this question, I will need to firstly separate the differences between sequential networks like RNNs and Transformers, which then introduces this problem nicely.

In RNNs, we feed in data (let's say a sequence of words) into the model in a sequential manner. This means that in the context of inputting in a sequence of words, the model does arguably obtain the order the tokens as it is fed in one by one.

With transformers, on the other hand, all of the words in the sequence are fed in all at once. This means that, so far, transformers do not have any notion of word ordering. Therefore, we need positional embeddings to tell the model where each word belongs in the sequence.

I believe the reason why we add them to word embeddings is because we want to maintain a similar input into the model as an RNN, which takes in word embeddings as its input as well. I think your question is a very good one to ask, and maybe you should experiment with having a more compressed word embedding with its positional embedding and compare your approach against the more "traditional" approach and see what results you yield. I'll be excited to see them.