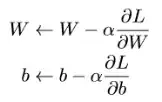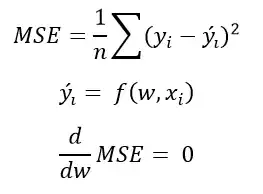My cost/loss function drops drastically and approaches 0, which looks a sign of convergence. But the weights are still changing in a visible way, a lot faster than the cost function. Should I ensure the weights converge too?
Some details: I just calculated for 1 epoch. My loss function is mean square difference. I use no optimizer. I tried several experiments and different initial weights but all got converged loss function with ever-changing weights.
The weights in a model do not need to converge to stop training.
One possible explanation is that the model error surface has a big, wide valley. If that is the case, the loss function would be low throughout the valley but there would be many weight combinations that would all yield similar performance on the training dataset. Once a model has reached an acceptable loss function value there is no reason to continue training, just take any set of weight values.
Can you provide us with more info? What optimizer do you use and with what parameters, how many epochs and experiments did you run, what is your loss function?...
i just calculated for 1 epoch
This doesn't make any sense for conclussion you wrote in this post.
My cost/loss function drops drastically and approaches 0
When you didn't use any optimizer to optimize the loss as you have said, Technically it's not possible for the cost/loss function to drop drastically and approach zero. It's only because of the optimizer that the model works with the objective of reducing cost/error or in simpler terms from gradient descent hill analogy, optimizer finds"descending the hill in what way accounts for the most reduction in error". Your model just stays at the top of the hill forever!!!. The loss is just a number for your model.
Since there is no optimizer in your code, It's technically not possible that "cost/loss function drops drastically and approaches 0".Your model's loss stays in point B forever
But the weights are still changing in a visible way, a lot faster than the cost function
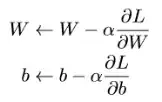
The above given are the update equations. Due to the random prediction of your model, At every batch, Some points tend to get predicted as correct class randomly. This accounts for some very small reduction in loss. And this change in loss is updated on the weights using the equation above. And so you may see random changes in weights for each batch. The overall effect of this change is negligible.
I've also made some real examples with mnist data which I computed without optimizer and the results are as follows:
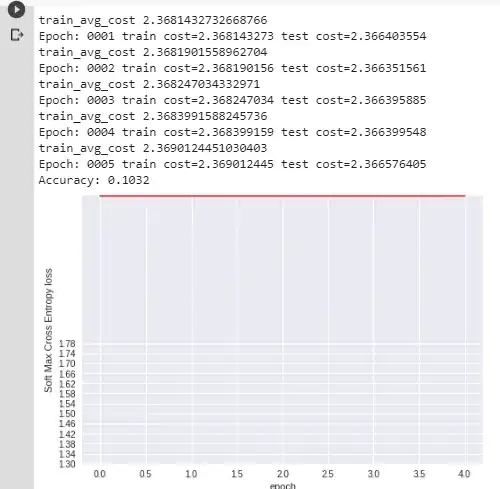
Here you can clearly see the red line(loss) stays on top of the graph forever. I had a batch size of 5 and ran it for 5 epochs
Convergence of the weights are not necessary (although in the case of converging the loss to a very low value, it can be a good news)
In fact, all learning methods are professional and fast search algorithms which search for the best answer for a problem using numerical methods in order to minimize the loss value. This means your problem maybe has not a unique answer.
On the other hand the update rate of the weights is directly related to the learning rate value. So, by assuming what I say, the wights must change in every episode but may be in that domain of change they resulted into a same result.
This equation can have several answers.
