I need help because I'm just new to machine learning and I do not know if k-nearest neighbors algorithm can be used to identify the appropriate program(s) for Student 11 in the table below.
The school subjects (Math, English, etc.) are the features, while the 'Program' column has the class labels A, B, and C. The binary values represent the interest of a student in the subjects. Can K-NN algorithm find the similar students based on the binary variables in the table?
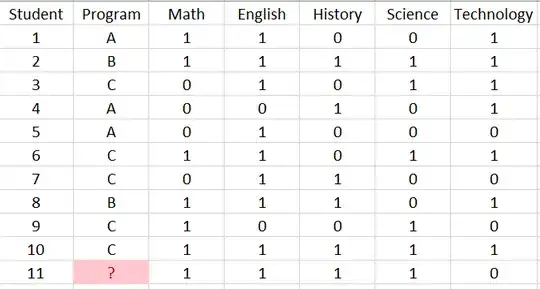
Yes, you just have to find a suitable distance metric, instead of using the default Euclidean distance. Euclidean distance will work, but it loses a lot of its positive points when used on a non-euclidean space.
For you specific case, the Jaccard distance basically measures how many 1's are equal on both instances, ignoring the dimensions where both are 0's. This gives an interpretation like "if a program has a course, but the other doesn't, then they are dissimilar". Jaccard index is very useful in high-dimensional boolean matrices, such as generated by one-hot encodings.
Other more intuitive choice is the perfect match distance, which would simply measure how many dimensions are different for the two instances and can be easily computed by $\sum_{i=1}^n |X_i - Y_i|$. In this case, the interpretation becomes similar to "if both programs have a course, or both program don't have a course, then they're similar".
However, be careful with the K value of your K-NN. You only have two instances of class B, so you will have to choose 1 or 2 (technically at most 3) for the value of K.
Whoa, there's a much simpler way to find the right program given the five scores.
The sample space is 2^5 = 32 (just like five flips of a fair coin). Each of those must be mapped to a program A-C, and because 32 > 3, more than one of the possible combinations is mapped to at least one of the programs.
All else being equal, most programs are mapped by about 10 combinations. But there must have been a rule to associate each combination with a program, no?
So, all you need is a key, value hash table. Probably the simplest thing to do is to concatenate the subjects into five letter strings ('11011') to use as keys, so a minimal dictionary in Python would look like
sorting_hat = {'11011': 'C'}
