I am trying to understand an article Backpropagation In Convolutional Neural Networks
But I can not wrap my head around that diagram: 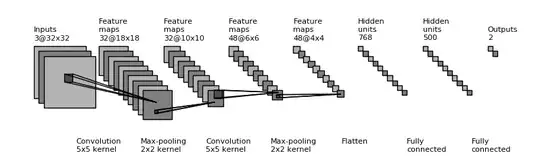
The first layer has 3 feature maps with dimensions 32x32. The second layer has 32 feature maps with dimensions 18x18. How is that even possible ? If a convolution with a kernel 5x5 applied for 32x32 input, the dimension of the output should be $(32-5+1)$ by $(32-5+1)$ = $28$ by $28$.
Also, if the first layer has only 3 feature maps, the second layer should have multiple of 3 feature maps, but 32 is not multiple of 3.
Also, why is the size of the third layer is 10x10 ? Should it be 9x9 instead ? The dimension of the previouse layer is 18x18, so 2x2 max pooling should reduce it to 9x9, not 10x10.