validation_curve differs from cross_val_score?

Question

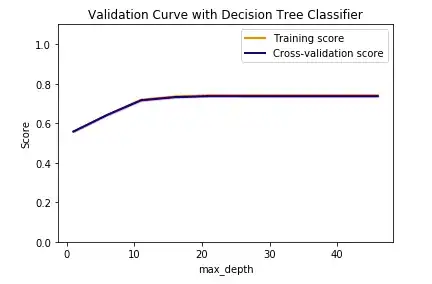
I'm trying to see how well a decision tree classifier performs on my input. For this I'm trying to use the validation and learning curves and SKLearn's cross-validation methods. However, they differ, and I don't know what to make of it.

The validation curve shows up as follows:

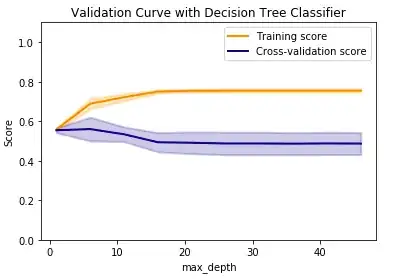
Based on varying the maximum depth parameter, I'm getting worse and worse cross-val scores. However, when I try the cross_val_score, I get ~72% accuracy reliably:

While I was using the default tree depth for clf here, it still puzzles me how the validation curve never reaches even 0.6, but the cross-val scores are all above 0.7. What does this mean? Why is there a discrepancy?

Code for reference below.

For the Validation curve:

import matplotlib.pyplot as plt
import numpy as np

from sklearn.datasets import load_digits
from sklearn.svm import SVC
from sklearn.model_selection import validation_curve

X, y = prepareDataframeX.values, prepareDataframeY.values.ravel()

param_range = np.arange(1, 50, 5)
train_scores, test_scores = validation_curve(
    DecisionTreeClassifier(class_weight='balanced'), X, y, param_name="max_depth", param_range=param_range,
    cv=None, scoring="accuracy", n_jobs=1)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)

plt.title("Validation Curve with Decision Tree Classifier")
plt.xlabel("max_depth")
#plt.xticks(param_range)
plt.ylabel("Score")
plt.ylim(0.0, 1.1)
lw = 2
plt.plot(param_range, train_scores_mean, label="Training score",
             color="darkorange", lw=lw)
plt.fill_between(param_range, train_scores_mean - train_scores_std,
                 train_scores_mean + train_scores_std, alpha=0.2,
                 color="darkorange", lw=lw)
plt.plot(param_range, test_scores_mean, label="Cross-validation score",
             color="navy", lw=lw)
plt.fill_between(param_range, test_scores_mean - test_scores_std,
                 test_scores_mean + test_scores_std, alpha=0.2,
                 color="navy", lw=lw)
plt.legend(loc="best")
plt.show()

For the cross-val scores:

clf = DecisionTreeClassifier(class_weight='balanced')
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.33, random_state=42)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
clf.score(X_test, y_test)

UPDATE A comment has been asked about shuffling. When I shuffle the data by

X, y = prepareDataframeX.values, prepareDataframeY.values.ravel()
indices = np.arange(y.shape[0])
np.random.shuffle(indices)
X, y = X[indices], y[indices]

I get:

Which makes even less sense to me. What does this mean?

Green Falcon · Accepted Answer · 2018-01-23T13:23:33.393

First of all, you have to shuffle your data because it seems that the model has learned a special pattern in the training data which has not occurred in the test data so much. After that, suppose that you get a validation curve like the current one. As you can see, Increasing the value of depth, does not change the learning. The two lines are parallel. In cases which each of the lines may have intersection, the upper line has negative slope and the lower one has positive slope, in the future on seen levels, you may want to increase the number of levels, not in this case.

Having same error, means that you are not over-fitting. but as you can see the amount of learning is not too much which means that you are having high bias problem, which means you have not learned the problem so well. In this case means that your current feature space maybe has high Bayes error which means that there are samples which have same features and different labels. Actually the distributions of different classes overlap.

There is something to argue about decision trees. If you have numerical features which are continuous, you may not have exactly same input patterns but they have overlap in their range.

validation_curve differs from cross_val_score?

1 Answers1