Relation between convolution in math and CNN

Question

I've read explanation of convolution and understand it to some extent. Can somebody help me understand how this operation relates to convolution in Convolutional Neural Nets? Is filter like function g which applies weight?

Answer 1

Using the notation from the wikipedia page, the convolution in a CNN is going to be the kernel $g$ of which we will learn some weights in order to extract the information we need and then perhaps apply an activation function.

Discrete convolutions

From the wikipedia page the convolution is described as

$(f * g)[n] = \sum_{m=-\inf}^{\inf} f[m]g[n-m]$

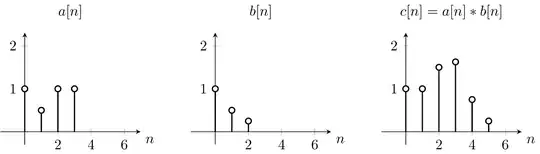
For example assuming $a$ is the function $f$ and $b$ is the convolution function $g$,

To solve this we can use the equation first we flip the function $b$ vertically, due to the $-m$ that appears in the equation. Then we will calculate the summation for each value of $n$. Whilst changing $n$, the original function does not move, however the convolution function is shifted accordingly. Starting at $n=0$,

$c[0] = \sum_m a[m]b[-m] = 0 * 0.25 + 0 * 0.5 + 1 * 1 + 0.5 * 0 + 1 * 0 + 1 * 0 = 1$

$c[1] = \sum_m a[m]b[-m] = 0 * 0.25 + 1 * 0.5 + 0.5 * 1 + 1 * 0 + 1 * 0 = 1$

$c[2] = \sum_m a[m]b[-m] = 1 * 0.25 + 0.5 * 0.5 + 1 * 1 + 1 * 0 + 1 * 0 = 1.5$

$c[3] = \sum_m a[m]b[-m] = 1 * 0 + 0.5 * 0.25 + 1 * 0.5 + 1 * 1 = 1.625$

$c[4] = \sum_m a[m]b[-m] = 1 * 0 + 0.5 * 0 + 1 * 0.25 + 1 * 0.5 + 0 * 1 = 0.75$

$c[5] = \sum_m a[m]b[-m] = 1 * 0 + 0.5 * 0 + 1 * 0 + 1 * 0.25 + 0 * 0.5 * 0 * 1 = 0.25$

As you can see that is exactly what we get on the plot $c[n]$. So we shifted around the function $b[n]$ over the function $a[n]$.

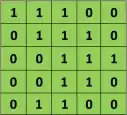
2D Discrete Convolution

For example, if we have the matrix in green

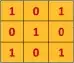
with the convolution filter

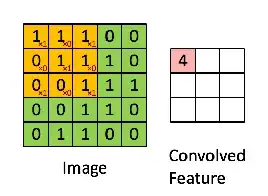
Then the resulting operation is a element-wise multiplication and addition of the terms as shown below. Very much like the wikipedia page shows, this kernel (orange matrix) $g$ is shifted across the entire function (green matrix) $f$.

taken from the link that @Hobbes reference. You will notice that there is no flip of the kernel $g$ like we did for the explicit computation of the convolution above. This is a matter of notation as @Media points out. This should be called cross-correlation. However, computationally this difference does not affect the performance of the algorithm because the kernel is being trained such that its weights are best suited for the operation, thus adding the flip operation would simply make the algorithm learn the weights in different cells of the kernel to accommodate the flip. So we can omit the flip.

Answer 2

Yes they are related. As an example, consider Gaussian smoothing (en.wikipedia.org/wiki/Gaussian_blur) which is a convolution with a kernel of Gaussian values. A CNN learns the weights of filters (i.e. kernels), and thus can learn to perform smoothing if needed.

Answer 3

Although CNN stands for convolutional neural networks, what they do is named cross-correlation in mathematics and not convolution. Take a look at here.

Now, before moving on there is a technical comment I want to make about cross-correlation versus convolutions and just for the facts what you have to do to implement convolutional neural networks. If you reading different math textbook or signal processing textbook, there is one other possible inconsistency in the notation which is that, if you look at the typical math textbook, the way that the convolution is defined before doing the element Y's product and summing, there's actually one other step ...