Suppose that I am interested in three classes $c_1$, $c_2$, $c_3$. But my dataset actually contains several more real classes $(c_j)_{j=4}^n$.
The obvious answer is to define a new class $\hat c_4$ that refers to all classes $c_j$, $j>3$ but I suspect this is not a good idea since the samples in $\hat c_4$ will be rare and not very similar to each other.
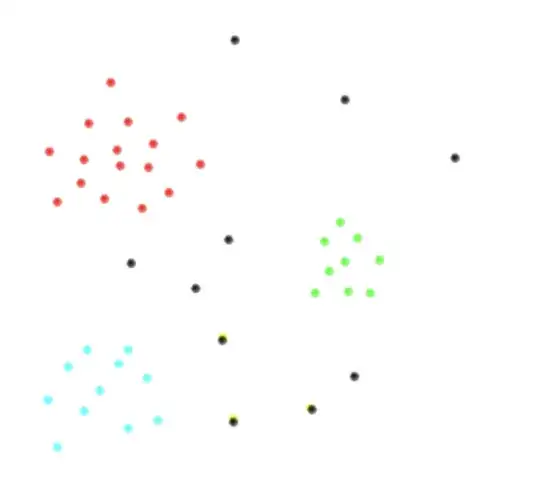
To visualize what I'm trying to say, suppose I have the following two variable space and the classes $c_1$, $c_2$, $c_3$, $\hat c_4= \bigcup_{j=4}^n c_j$ are depicted in red, til, green and black respectively. This is how I suspect my data would look like.
Is there any standard way to approach this problem? What would be the most efficient classifier and why?