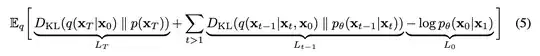In the Denoising Diffusion Probabilistic Models paper (https://arxiv.org/abs/2006.11239), the rate-distortion plot is computed assuming access to a protocol that can transmit samples $(x_T, ... x_0)$. This is then used to construct Algorithm3 and Algorithm4 in the paper, and the claim is that Eqn 5 (pasted below) gives the total number of bits transmitted on average.
I am confused how this is possible?
e.g. if we restrict ourselves to just transmitting $x_T$, and if $p(x_T)$ and $q(x_T|x_0)$ are exactly same (e.g. both isotropic Gaussians), we cannot send $D_{KL}(q(x_T|x_0) || p(x_T)) = 0$ bits to reconstruct $x_T$ at the reciever. It seems we would need at least the $H(x_T)$ bits to be sent where $H$ is the entropy function. Wikipedia entry on KL divergence also seems to agree with this interpretation: https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence#Introduction_and_context.
If Algorithm3 and Algorithm4 are just trying to send a message such that the receiver has a random variable $y_T$ such that $x_T$ and $y_T$ have exactly the same distribution, then this seems possible to achieve with $D_{KL}(q(x_T|x_0) || p(x_T))$ bits for the first step. However in this case, doesn’t the logic break down at the next step? i.e. $p(x_{T-1}|x_T)$ will in general be very different from $p(y_{T-1}|y_T)$.