2

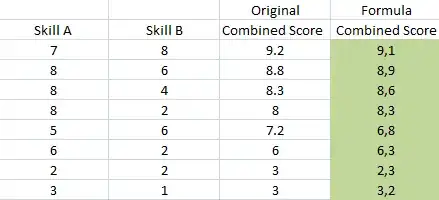
I want to evaluate individuals on a scale of 1 to 10 based on their skills in two areas, Skill A and Skill B. Our goal is to reward those who possess skills in both areas by giving them a higher Combined Score. However, if someone has skills in only one area, their evaluation should not be penalized.

Scoring Method:

Combine the scores from Skill A and Skill B. If an individual has high scores in both skills, they receive a bonus to their Combined Score. If an individual has a high score in only one skill, their score remains the same or is slightly adjusted.

Examples:

Skill A Skill B Combined Score
7 8 9.2
8 6 8.8
8 4 8.3
8 2 8
5 6 7.2
6 2 6
2 2 3
3 1 3

Question:

What would be an effective method to calculate the Combined Scores for these individuals, ensuring that those with high scores in both areas are rewarded, while those with skills in only one area are not penalized? Are there any specific formulas or approaches that could be recommended for this evaluation process?

Damian
  • 21
  • 2

2 Answers2

2

One simple solution could be to take:

min( max(A, B) + 0.15 * min(A, B), 10 )

enter image description here

One limitation is when there is one 10 then the Combined Score will be 10 (even if the other is 1 or 10)

rehaqds
  • 1,801
  • 4
  • 13
2

I suggest to use linear regression to solve this problem. First you have to sort the skills and then you can use the linear regression model from sklearn to get the coefficients.

import numpy as np
from sklearn.linear_model import LinearRegression

x = np.array([[7, 8], [8, 6], [8, 4], [8, 2], [5, 6], [6, 2], [2, 2], [3, 1]])
x_sorted = np.sort(x)
y = np.array([9.2, 8.8, 8.3, 8.0, 7.2, 6.0, 3.0, 3.0])
reg = LinearRegression().fit(x_sorted, y)


print(reg.coef_)
print(reg.intercept_)
print(reg.predict(x_sorted))

The final formula is:

0.52 + 0.30 * min(A, B) + 0.83 * max(A, B)
Skill A Skill B Combined Score Predicted Score
7 8 9.2 9.25
8 6 8.8 8.95
8 4 8.3 8.36
8 2 8 7.77
5 6 7.2 6.99
6 2 6 6.10
2 2 3 2.78
3 1 3 3.31

Notes:

  • You can manually fine tune the obtained formula for further improvements or additional requirements
  • You can add more data to improve poor predictions on new skill values or corner cases
  • The previous answer is a manual solution of the same linear regression problem and was helpful to get the general solution
CSD
  • 51
  • 3